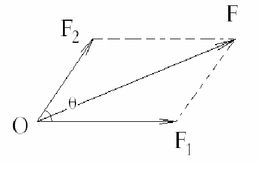
力的平行四邊形法則
選自《中學教學實用全書》共點力的合成法則．
這一法則通常表述為：以表示兩個共點力的有向線段為鄰邊作一平行四邊形，該兩鄰邊之間的對角線即表示兩個力的合力的大小和方向．
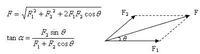平行四邊形法則由力的平行四邊形法則可知，兩個共點力的合力不僅與兩個力的大小有關，且與兩個力的夾角有關．當兩個力的大小一定時，其合力的大小將隨兩個力夾角的改變在兩個力之和與兩個力之差範圍內變化．
運用平行四邊形法則求一共點力系的合力時，可採用依次合成的方法．例如求三個共點力F1 、F2 和F3 的合力F，可先求出 F1和F2 的合力F4 ，然後再求出F3 和F4 的合力F ， 即為三個共點力的合力F．平行四邊形法則不僅是共點力的合成法則，也是一切矢量合成共同遵循的法則．
定義
求兩個互成角度的共點力的合力，可以用表示這兩個力的線段為鄰邊作平行四邊形，這兩個鄰邊之間的對角線就表示合力的大小和方向，這種方法就叫做“力的平行四邊形法則”。
詳解
我們知道加、減、乘、除的算術運算，是用來計算兩個以上的標量的，如質量、面積、時間等。例如，求密度就要用體積去除質量。標量之間的運算不需要特別的手續，只有一個要求，那就是單位要一致。
但是，矢量相加就要用特別的方法，因為被加的量既有一定數值，又有一定的方向，相加時兩者要同時考慮。在力學中經常遇到的矢量有位移、力、速度、加速度、動量、衝量、力矩、角速度和角動量等。
矢量的加法有兩種：其一即所謂三角形法則；另一方法即平行四邊形法則，它們本質是一樣的。若用三角形法則求總位移似乎直觀些，而用平行四邊形法則求力的合成好像更便於理解。
若用3毫米代表1千米。如圖1－1所示的那樣，以紙面上某點A作為出發點，作矢量 ，長3厘米，代表向東10公里；然後在A點再作 同 成45°角，長1.5厘米，代表向東北5千米。然後，過B作BC平行AD，過D作DC平行AB，由此便得到平行四邊形ABCD。從A向C作射線 ，這就是總位移矢量。
應注意物體A點不是受 F1、F2 、F3 三個力的作用。因為F2 是F1 和F3 的合力，表示 的作用效果與 、 的共同作用效果是一樣的。因此可以用 代替 和 的共同作用，但絕不能把 當成作用在物體上的第三個力。在分析物體受力情況時，不能同時考慮合力與分力對物體的作用。例如，當物體沿光滑斜面下滑時，不能說物體除受到重力和斜面的彈力作用外，還受到一個下滑力的作用。因為下滑力是重力沿斜面平行方向的分力，所以，只能說“在光滑斜面上下滑的物體，受到重力和斜面彈力的作用”。有的人認為：“合力總比分力大”。我們可利用求合力的平行四邊形法則，通過作圖可看到，合力的大小是隨兩分力夾角而變化的，絕不能說“合力一定要比分力大”。
一個矢量，只要遵守平行四邊形法則，可以分解為兩個，或無窮個。但是矢量的合成不同，兩個矢量只能合成為一個矢量。
驗證定則
同時用兩個力F1、F2拉橡皮繩，使橡皮繩伸長，改用一個力F′直接拉橡皮繩，使橡皮繩伸長，且使兩次橡皮繩伸長相同。由第1次兩個力F1、F2作圖得合力F，與第2次拉的拉力F′比較，即可驗證平行四邊形定則的正確性。實驗目的：驗證平行四邊形定則。
實驗器材：木板、白紙、彈簧秤（兩隻完全相同）、橡皮繩、長細線（兩根）三角板、刻度尺、圖釘（若干個）、量角器。
實驗步驟：
（1）把白紙用圖釘固定在木板上
（2）把橡皮繩連線好，另一端固定在木板上。記下此時橡皮繩的原長O點
（3）同時用兩個彈簧秤拉橡皮繩，使橡皮條伸長到某一位置O′，如圖，記錄兩彈簧測力計的讀數F1、F2，用鉛筆描O′點的位置及此時兩細繩的方向．
（4）作出第（3）步中兩力F1、F2的圖示，並用平行四邊形定則求出合力F。（5）用一隻彈簧秤拉橡皮繩，使橡皮繩與第（3）步中標記的位置O′重合，記下彈簧秤讀數F′和拉力方向，作出力的圖示。
（6）比較第（4）步中求得合力F與第（5）步中拉力F′是否吻合，F與F′的夾角不超過5°。（7）重複上述（3）～（6）二次，記錄數據注意事項：
1．位置不變：在同一次實驗中，使橡皮條拉長時結點的位置O′點一定要相同．
2．角度合適：用兩個彈簧測力計鉤住互成角度地拉橡皮條時，其F1、F2夾角不宜太小，也不宜太大，以60°～100°之間為宜．
4．統一標度：在同一次實驗中，畫力的圖示選定的標度要相同，並且要恰當選定標度，使力的圖示稍大一些．
合成法則
法則概念
這一法則通常表述為：以兩個共點力的有向線段為鄰邊作一平行四邊形，該兩鄰邊的對角線即表示兩個力合力的大小和方向．由力的平行四邊形法則可知，兩個共點力的合力不僅與兩個力的大小有關，且與兩個力的夾角有關．當兩個力的大小一定時，其合力的大小將隨兩個力夾角的改變在兩個力之和與兩個力之差範圍內變化．
運用平行四邊形法則求一共點力系的合力時，可採用依次合成的方法．例如求三個共點力F1、F2和F3的合力F，可先求出F1和F2的合力F4，然後再求出F3和F4的合力F，即為三個共點力的合力F．平行四邊形法則不僅是共點力的合成法則，也是一切矢量合成共同遵循的法則．
定義
求兩個互成角度的共點力的合力，可以用表示這兩個力的線段為鄰邊作平行四邊形，這兩個鄰邊之間的對角線就表示合力的大小和方向，這種方法就叫做“力的平行四邊形法則”。詳解
我們知道加、減、乘、除的算術運算，是用來計算兩個以上的標量的，如質量、面積、時間等。例如，求密度就要用質量(m)去除體積(V)。標量之間的運算不需要特別的手續，只有一個要求，那就是單位要一致。但是，矢量相加就要用特別的方法，因為被加的量既有一定數值，又有一定的方向，相加時兩者要同時考慮。在力學中經常遇到的矢量有位移、力、速度、加速度、動量、衝量、力矩、角速度和角動量等。矢量的加法有兩種：其一即所謂三角形法則；另一方法即平行四邊形法則，它們本質是一樣的。若用三角形法則求總位移會顯得直觀些，而用平行四邊形法則求力的合成則更便於理解。
若用3毫米代表1千米。如圖1－1所示的那樣，以紙面上某點A作為出發點，作矢量，長3厘米，代表向東10公里；然後在A點再作同成45°角，長1.5厘米，代表向東北5千米。然後，過B作BC平行AD，過D作DC平行AB，由此便得到平行四邊形ABCD。從A向C作射線，這就是總位移矢量。
應注意物體A點不是受F1、F2、F3三個力的作用。因為F2是F1和F3的合力，表示的作用效與、的共同作用效果是一樣的。因此可以用代替和的共同作用，但絕不能把當成作用在物體上的第三個力。在分析物體受力情況時，不能同時考慮合力與分力對物體的作用。例如，當物體沿光滑斜面下滑時，不能說物體除受到重力和斜面的彈力作用外，還受到一個下滑力的作用。因為下滑力是重力沿斜面平行方向的分力，所以，只能說“在光滑斜面上下滑的物體，受到重力和斜面彈力的作用”。有的人認為：“合力總比分力大”。我們可利用求合力的平行四邊形法則，通過作圖可看到，合力的大小是隨兩分力夾角而變化的，絕不能說“合力一定要比分力大”。
一個矢量，只要遵守平行四邊形法則，可以分解為兩個，或無窮個。但是矢量的合成則不同，兩個矢量只能合成為一個矢量。
