公式推導
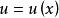 分部積分法
分部積分法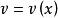 分部積分法
分部積分法 分部積分法
分部積分法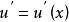 分部積分法
分部積分法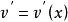 分部積分法
分部積分法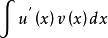 分部積分法
分部積分法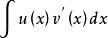 分部積分法
分部積分法分部積分法:設 及 是兩個關於 的函式,各自具有連續導數 及 ,且不定積分 存在,按照乘積函式求微分法則,則有 存在,且得 分部積分公式如下
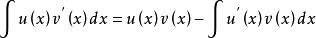 分部積分法
分部積分法證明:由
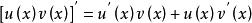 分部積分法
分部積分法或
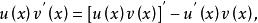 分部積分法
分部積分法對上式兩邊求不定積分,即得 分部積分公式,也將其簡寫為
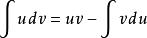 分部積分法
分部積分法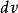 分部積分法
分部積分法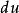 分部積分法
分部積分法如果將 和 用微分形式寫出,則亦可得出
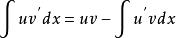 分部積分法
分部積分法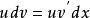 分部積分法
分部積分法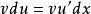 分部積分法
分部積分法上兩式就把 的積分轉化為 的積分,即將複雜的被積函式簡單化。
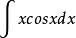 分部積分法
分部積分法例如,要求 ,則依分部積分法則,令
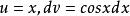 分部積分法
分部積分法如此
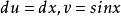 分部積分法
分部積分法則按上述公式有
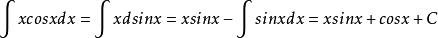 分部積分法
分部積分法四種典型模式
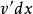 分部積分法
分部積分法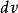 分部積分法
分部積分法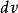 分部積分法
分部積分法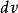 分部積分法
分部積分法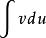 分部積分法
分部積分法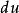 分部積分法
分部積分法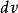 分部積分法
分部積分法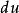 分部積分法
分部積分法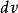 分部積分法
分部積分法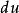 分部積分法
分部積分法一般地,從要求的積分式中將 湊成 是容易的,但通常有原則可依,也就是說不當的分部變換不僅不會使被積分式得到精簡,而且可能會更麻煩。分部積分法最重要之處就在於準確地選取 ,因為一旦 確定,則公式中右邊第二項 中的 也隨之確定,但為了使式子得到精簡,如何選取 則要依 的複雜程度決定,也就是說,選取的 一定要使 比之前的形式更簡單或更有利於求得積分。依照經驗,可以得到下面四種典型的模式。 記憶模式口訣:反(函式)對(數函式)冪(函式)三(角函式)指(數函式)。
模式一
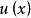 分部積分法
分部積分法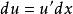 分部積分法
分部積分法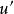 分部積分法
分部積分法 分部積分法
分部積分法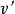 分部積分法
分部積分法 分部積分法
分部積分法通過對 求微分後, 中的 比 更加簡潔,而 與 的類型相似或複雜程度相當。
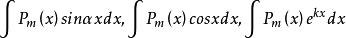 分部積分法
分部積分法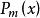 分部積分法
分部積分法 分部積分法
分部積分法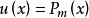 分部積分法
分部積分法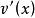 分部積分法
分部積分法例如,對於形如 的不定積分(其中 為 次多項式),由於對多項式求微分可以降次,且三角函式或指函式的積分則較容易求得,所以可以令 ,而將另一個函式看成 通過分部求得積分。
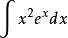 分部積分法
分部積分法例如 求
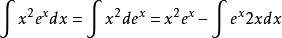 分部積分法
分部積分法首先,
對該式第二項再按此模式進行分部積分,得
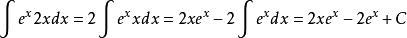 分部積分法
分部積分法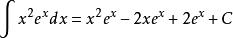 分部積分法
分部積分法故原式
模式二
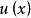 分部積分法
分部積分法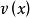 分部積分法
分部積分法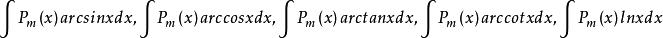 分部積分法
分部積分法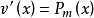 分部積分法
分部積分法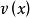 分部積分法
分部積分法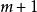 分部積分法
分部積分法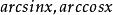 分部積分法
分部積分法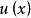 分部積分法
分部積分法通過對 求微分使得它的類型與 的類型相同或相近,然後將它們作為一個統一的函式來處理。例如對形如 等的積分,總是令 ,則 則為一個 次的多項式,另一個函式( 等)看成 。通過分部積分,很容易求出不定積分。
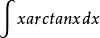 分部積分法
分部積分法例如,求
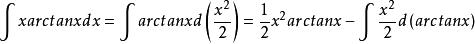 分部積分法
分部積分法而該式第二項為
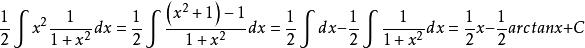 分部積分法
分部積分法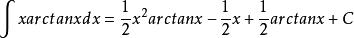 分部積分法
分部積分法故原積分式
模式三
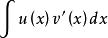 分部積分法
分部積分法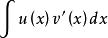 分部積分法
分部積分法利用有些函式經一次或二次求微分後不變的性質,通過一次或二次分部積分後,使等式右端再次產生 ,只要它的係數不為1,就可以利用解方程的方法求出原積分 。
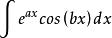 分部積分法
分部積分法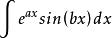 分部積分法
分部積分法例如,對於積分 和
按法則對他們進行分部積分得
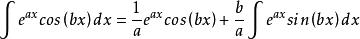 分部積分法
分部積分法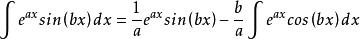 分部積分法
分部積分法這樣,所求積分均由另一個積分所表示出來,將這兩式相加和相減(即解方程)得到所求積分表達式
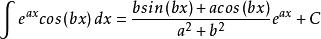 分部積分法
分部積分法以及
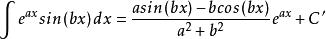 分部積分法
分部積分法這兩個通用表達式就可以求出該類型的所有積分式,比如
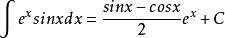 分部積分法
分部積分法模式四
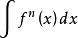 分部積分法
分部積分法 分部積分法
分部積分法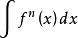 分部積分法
分部積分法對某些形如 的不定積分,利用分部積分可降低 的次數,求得遞推公式,然後再次利用遞推公式,求出 。
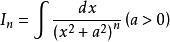 分部積分法
分部積分法例如,對於積分
 分部積分法
分部積分法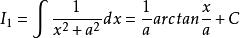 分部積分法
分部積分法當 時,
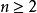 分部積分法
分部積分法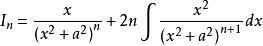 分部積分法
分部積分法當 時,
而該式的第二項又可變換為
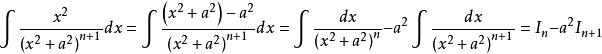 分部積分法
分部積分法將其帶入上式,則得到
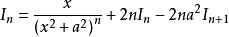 分部積分法
分部積分法故
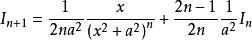 分部積分法
分部積分法最後,得到統一的遞推關係式
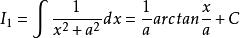 分部積分法
分部積分法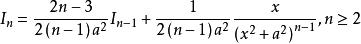 分部積分法
分部積分法定積分
與不定積分的分部積分法一樣,可得
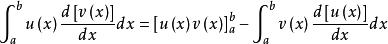 分部積分法
分部積分法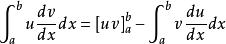 分部積分法
分部積分法簡寫為
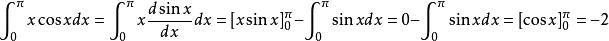 分部積分法
分部積分法例如
示例
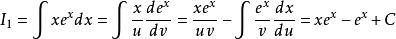 分部積分法
分部積分法例1:
例2 :
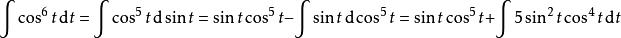 分部積分法
分部積分法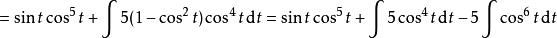 分部積分法
分部積分法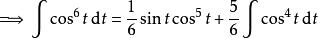 分部積分法
分部積分法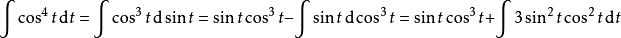 分部積分法
分部積分法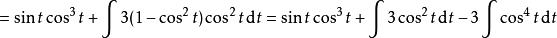 分部積分法
分部積分法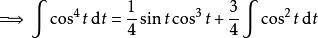 分部積分法
分部積分法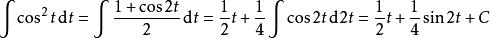 分部積分法
分部積分法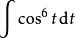 分部積分法
分部積分法回代即可得到 的值。

