概念
分布曲線是以變數值為橫坐標,以累積頻率[機率]為縱坐標的曲線圖,即機率分布函式的圖形。例如正態曲線等。
分布曲線使標準分數在實際運用時非常有用。知道了Z分數,就能立刻知道該分數是在均數以上還是在均數以下。又因為標準分數是根據標準差求得的,知道了標準分數也就知道了它出現的機率。比如,在整個常態分布中,有34%的分數位於從均數到1個標準差的區域內(0≤|Z|≤1),16%的分數位於分布的兩端超出1個標準差的區域(|Z|>1),大於2個標準差的分數隻占2。5%(|Z|>2)。
表示一個人的的得分在一個團體中的相對地位,可以在使用百分等級之外,選擇使用〝標準分數〞:Z分數和T分數。
也就是將原始分數轉換為一種以平均數為基準,以標準差為單位的距變數。以標準分數的優點來說:可以直接比較某生在不同考試中的相對地位或不同考生在不同考試中的相對地位。
常態分配
分布曲線一種機率分布。常態分配是具有兩個參數μ和σ2的連續型隨機變數的分布,第一參數μ是遵從常態分配的隨機變數的均值,第二個參數σ2是此隨機變數的方差,所以常態分配記作N(μ,σ2)。遵從常態分配的隨機變數的機率規律為取μ鄰近的值的機率大,而取離μ越遠的值的機率越小;σ越小,分布越集中在μ附近,σ越大,分布越分散。常態分配的密度函式的特點是:關於μ對稱,在μ處達到最大值,在正(負)無窮遠處取值為0,在μ±σ處有拐點。它的形狀是中間高兩邊低,圖像是一條位於x軸上方的鐘形曲線。當μ=0,σ2=1時,稱為標準常態分配,記為N(0,1)。μ維隨機向量具有類似的機率規律時,稱此隨機向量遵從多維常態分配。多元常態分配有很好的性質,例如,多元常態分配的邊緣分布仍為常態分配,它經任何線性變換得到的隨機向量仍為多維常態分配,特別它的線性組合為一元常態分配。
常態分配最早由A.棣莫弗在求二項分布的漸近公式中得到。C.F.高斯在研究測量誤差時從另一個角度導出了它。P.S.拉普拉斯和高斯研究了它的性質。
生產與科學實驗中很多隨機變數的機率分布都可以近似地用常態分配來描述。例如,在生產條件不變的情況下,產品的強力、抗壓強度、口徑、長度等指標;同一種生物體的身長、體重等指標;同一種種子的重量;測量同一物體的誤差;彈著點沿某一方向的偏差;某個地區的年降水量;以及理想氣體分子的速度分量,等等。一般來說,如果一個量是由許多微小的獨立隨機因素影響的結果,那么就可以認為這個量具有常態分配(見中心極限定理)。從理論上看,常態分配具有很多良好的性質,許多機率分布可以用它來近似;還有一些常用的機率分布是由它直接導出的,例如對數常態分配、t分布、F分布等。
常態分配套用最廣泛的連續機率分布,其特徵是“鍾”形曲線。
機率分布
機率分布,是機率論的基本概念之一,主要用以表述隨機變數取值的機率規律。為了使用的方便,根據隨機變數所屬類型的不同,機率分布取不同的表現形式。事件的機率表示了一次試驗某一個結果發生的可能性大小。若要全面了解試驗,則必須知道試驗的全部可能結果及各種可能結果發生的機率,即必須知道隨機試驗的機率分布。
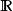 分布曲線
分布曲線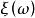 分布曲線
分布曲線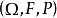 分布曲線
分布曲線機率分布律[law of probability distribution]簡稱機率律或機率分布。上描述隨機變數取值規律的機率測度。假定是機率空間上的隨機變數則由
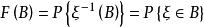 分布曲線
分布曲線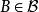 分布曲線
分布曲線 分布曲線
分布曲線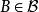 分布曲線
分布曲線 分布曲線
分布曲線 分布曲線
分布曲線所定義的上的集函式 F 是一個機率測度,稱為隨機交量的機率分布律。對於任何隨機變數落入B中的機率可通過計算B 的測度F(B) 得出這就是說機率分布F 完全刻畫了取值的機率規律。
機率密度
機率指事件隨機發生的機率,對於均勻分布函式,機率密度等於一段區間(事件的取值範圍)的機率除以該段區間的長度,它的值是非負的,可以很大也可以很小。
對於隨機變數X的分布函式F(x),如果存在非負可積函式f(x),使得對任意實數x,有
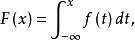 分布曲線
分布曲線則X為連續型隨機變數,稱f(x)為X的機率密度函式,簡稱為機率密度。
單純的講機率密度沒有實際的意義,它必須有確定的有界區間為前提。可以把機率密度看成是縱坐標,區間看成是橫坐標,機率密度對區間的積分就是面積,而這個面積就是事件在這個區間發生的機率,所有面積的和為1。所以單獨分析一個點的機率密度是沒有任何意義的,它必須要有區間作為參考和對比。
