人物簡介
阿貝爾是挪威數學家。生於挪威西南海岸斯塔萬格附近的小島芬島(Finno¨y)，卒於阿倫達爾(Arendal)附近的弗魯蘭(Froland)。父親是一個基督教牧師。阿貝爾幼年喪父，家境貧困，但他從小酷愛數學。16歲起自學當時的數學名著，中學時被譽為“數學迷”，得到教師霍爾姆博(Holmboe，B.M.)的賞識和資助。1821年以公費考入克里斯蒂安尼亞(Christiania)大學，1825年大學畢業後，獲得獎學金前往柏林和巴黎留學並謀職。在德國期間，他結識了克雷爾(Crelle，A.L.)，他們共同創辦了《克雷爾數學雜誌》，並在前三卷上發表了22篇有關方程論、橢圓函式論和冪級數方面的著名論文，使《克雷爾數學雜誌》獲得很高的聲譽.在巴黎他又寫出一批重要論文。1827年回國，在克里斯蒂安尼亞大學任教，不久患肺結核，1829年被聘為柏林大學教授，但未到任即病逝，年僅27歲。
阿貝爾一生雖然短暫，卻在數學史上留下了光輝的一頁。自從16世紀三、四次方程得到解決之後，五次以上方程的根式求解問題吸引著眾多的科學家。200多年未能成功，這使人們悟到了它的不可能性，在拉格朗日(Lagrange，J.-L.)和魯菲尼(Ruffini，P.)之後，阿貝爾進一步嚴格地證明了一般五次方程不可能用根式求解，開闢了近世代數方程論的道路，採用了包括群論和方程的超越函式解法.1826年，他在《克雷爾數學雜誌》創刊號上發表了震動數學界的論文《論代數方程，證明一般五次方程的不可解性》。他還同德國數學家雅可比(Jacobi，C.G.J.)共同奠定了橢圓函式論的基礎，創立了數學的一個新分支。阿貝爾發現了橢圓函式的加法定理、雙周期性，引進了阿貝爾積分。此外，在交換群、二項級數的嚴格理論、級數求和等方面都有突破性貢獻，但可惜他的論文的價值沒有及時被學術界所認識。
施洛德函式方程
施洛德函式方程是一類函式方程。函式方程：
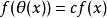阿貝爾函式方程稱為施洛德函式方程，其中θ(x)是已知函式，c是常數。如果f(x)是一特解(f≠0)，則其通解為f(x)=f(x)φ(x)，其中φ(x)是φ(θ(x))=φ(x)的通解。假設存在點a使得θ(a)=a， 並且θ(x)和f(x)在點a的鄰域內可微，於是有f′(a)=0或θ′(a)=c。考查θ′(a)=c的情形，若θ(x)在x=a處二次可微，且|c|<1， 那么在x=a的鄰域中序列{(θ(x)-a)c}一致收斂，θ(x)=x，θ(x)=θ(θ(x))(n=1，2，…)，它的極限f(x)就是方程(1)的一個解.如果|c|>1，則令θ(x)=u， 那么在u=a的鄰域f(θ(u))=cf(u)，這就化為|c|<1的情形了。
方程介紹
阿貝爾函式方程(Abel functional equation)是施洛德函式方程的一種變形。方程：
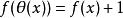阿貝爾函式方程稱為阿貝爾函式方程。θ(x)也是已知函式。如果令exp f(x)=φ(x)，則得到施洛德方程：
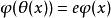阿貝爾函式方程再考慮方程：
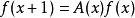阿貝爾函式方程(A(x)是已知函式)，如果令log f(x)=φ(x)，則得如下差分方程：
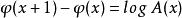阿貝爾函式方程解此差分方程即可得到原方程的解。
等效
上述這些方程式是等效的。假設α是可逆函式，則第二個方程可以寫成：
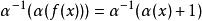阿貝爾函式方程
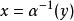阿貝爾函式方程將，上式可以重寫為：
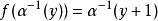阿貝爾函式方程
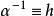阿貝爾函式方程
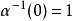阿貝爾函式方程假設f(x)函式已知，目標是用方程解函式方程，滿足初始條件。
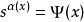阿貝爾函式方程
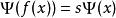阿貝爾函式方程做如下變數替換：，對一個實參數S，將阿貝爾方程改寫為施洛德方程：。
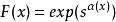阿貝爾函式方程
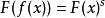阿貝爾函式方程用做替換，將阿貝爾方程改寫為Böttcher方程：。
另外，阿貝爾方程是轉換方程的特殊情況：
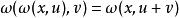阿貝爾函式方程
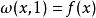阿貝爾函式方程
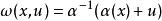阿貝爾函式方程例如對，
阿貝爾函式α(X)進一步證明了的移位運算元的正則坐標。
