定義
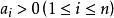 冪平均不等式
冪平均不等式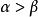 冪平均不等式
冪平均不等式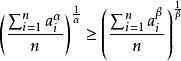 冪平均不等式
冪平均不等式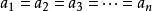 冪平均不等式
冪平均不等式冪平均不等式:,且,則有成立,若且唯若時取等號。
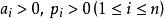 冪平均不等式
冪平均不等式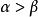 冪平均不等式
冪平均不等式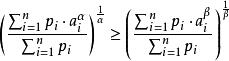 冪平均不等式
冪平均不等式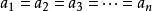 冪平均不等式
冪平均不等式加權的形式:設,且,則有成立,若且唯若時取等號。
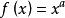 冪平均不等式
冪平均不等式其證明只需用到數學分析里的琴生不等式(即上下凸性),取輔助函式
性質
冪的指數越大,則均值不等式的值越大

冪平均不等式是在數學不等式的證明中常用的不等式,多次出現在省份高中數學聯賽、全國高中數學聯賽、CMO、IMO的代數問題中。
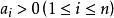 冪平均不等式
冪平均不等式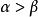 冪平均不等式
冪平均不等式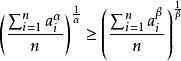 冪平均不等式
冪平均不等式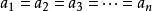 冪平均不等式
冪平均不等式冪平均不等式:,且,則有成立,若且唯若時取等號。
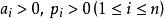 冪平均不等式
冪平均不等式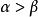 冪平均不等式
冪平均不等式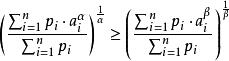 冪平均不等式
冪平均不等式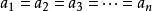 冪平均不等式
冪平均不等式加權的形式:設,且,則有成立,若且唯若時取等號。
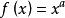 冪平均不等式
冪平均不等式其證明只需用到數學分析里的琴生不等式(即上下凸性),取輔助函式
冪的指數越大,則均值不等式的值越大
冪平均(power mean)也叫廣義平均(generalized mean)或赫爾德平均(Hölder mean),是畢達哥拉斯平均(包含了算術、幾何...
定義 性質 特例 不等式的證明 推廣”、小於號“
定義 基本性質 常用定理 定理口訣 注意事項不等式分為嚴格不等式與非嚴格不等式。一般地,用純粹的大於號、小於號“>”“<”連線的不等式稱為嚴格不等式,用不小於號(大於或等於號)、不大於號(小於或等...
定義 基本性質 常用定理 定理口訣 注意事項設ai
一般形式 加權形式 證明簡述重要不等式,是指在初等與高等數學中常用於計算與證明問題的不等式。包括,排序不等式、均值不等式、完全的均值不等式、冪平均不等式、權方和不等式、柯西不等式、...
柯西不等式 排序不等式 切比雪夫不等式 琴生不等式 均值不等式重要不等式,是指在初等與高等數學中常用於計算與證明問題的不等式。包括,排序不等式、均值不等式、完全的均值不等式、冪平均不等式、權方和不等式、柯西不等式、...
1.柯西不等式 2.排序不等式 3.切比雪夫不等式 4.琴生不等式 5.均值不等式平均數不等式,或稱平均值不等式、均值不等式,是數學上的一組不等式,也是基本不等式的推廣。
定義 證明方法 參見算術-幾何平均值不等式,簡稱算幾不等式,是一個常見而基本的不等式,表現了算術平均數和幾何平均數之間恆定的不等關係。
介紹 證明 例子 推廣 參見《數列與不等式》是2014-1-1 出版的圖書,作者是甘志國 。
作品信息 內容提要 目錄