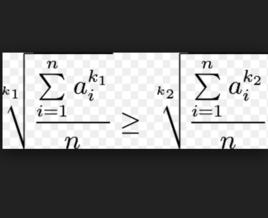
定義
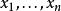 冪平均
冪平均若p是一非零實數,可定義實數 的p次冪平均為
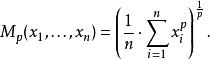 冪平均
冪平均性質
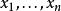 冪平均
冪平均 冪平均
冪平均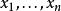 冪平均
冪平均(1)和所有平均一樣,冪平均是各參數的一次齊次函式。即若b是一個正實數,則 指數為 p 的冪平均等於b倍的冪平均。
(2)與幾何算術平均一樣,這種平均的計算可以分解成同樣大小的子塊來計算。
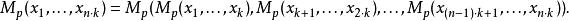 冪平均
冪平均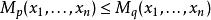 冪平均
冪平均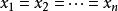 冪平均
冪平均(3)一般地,如果 p<q,則且這兩個平均相等若且唯若。這由事實
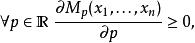 冪平均
冪平均得出,上述不等式可由琴生不等式證明。
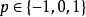 冪平均
冪平均特別地,對,冪平均不等式蘊含了畢達哥拉斯平均不等式以及算術幾何平均不等式。
特例
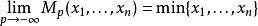 冪平均
冪平均-最小值,
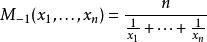 冪平均
冪平均-調和平均,
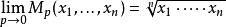 冪平均
冪平均-幾何平均,
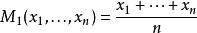 冪平均
冪平均-算術平均,
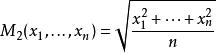 冪平均
冪平均-二次平均,
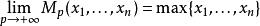 冪平均
冪平均-最大值。
不等式的證明
不等式之等價
假設指數 p與 q的冪平均間有不等式:
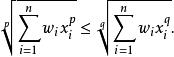 冪平均
冪平均則
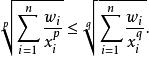 冪平均
冪平均我們在兩邊取倒數(正實數上的嚴格遞減函式,不等號反向):
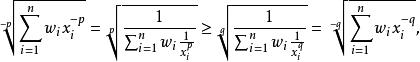 冪平均
冪平均我們得到了關於 - p與 - q的冪平均不等式,同樣的推理可以倒推,從而證明了兩個不等式等價,這在後面的證明中將用到。
幾何平均
對任何 q,指數為 q的冪平均與幾何平均之間的不等式為:
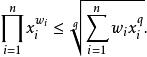 冪平均
冪平均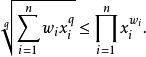 冪平均
冪平均(第一個不等式對正數 q,第二個對負數)
我們在兩邊取 q次冪:
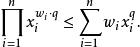 冪平均
冪平均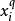 冪平均
冪平均兩種情形我們都得到關於的加權算術幾何平均不等式,這可以用琴生不等式證明,利用對數函式是凸函式的事實:
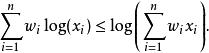 冪平均
冪平均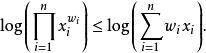 冪平均
冪平均兩邊取指數函式(嚴格遞增),我們得到了不等式:
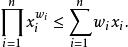 冪平均
冪平均從而對任何正數 q,下式成立:
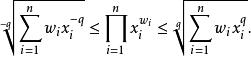 冪平均
冪平均因為此不等式對任何 q成立,足夠小同樣成立,可以將證明(利用洛必達法則),當 q趨於 0 時,左右兩邊趨於幾何平均, q趨於 0 時的冪平均是幾何平均:
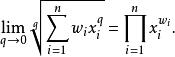 冪平均
冪平均冪平均不等式
我們將證明對任何 p< q如下不等式成立:
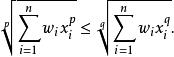 冪平均
冪平均如果 p是負數且 q是正數,不等式等價於上面已證過的
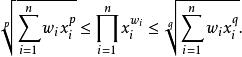 冪平均
冪平均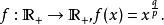 冪平均
冪平均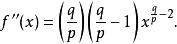 冪平均
冪平均對正數 p與 q的證明如下:定義函式 f是一個冪函式,所以有二階導數:,在 f的定義域內嚴格正,因為 q> p,從而我們知道 f是凸的。
利用這一點以及琴生不等式,我們得到:
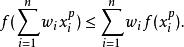 冪平均
冪平均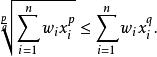 冪平均
冪平均兩邊取 1/ q次冪(遞增函式,因 1/q 為正數)我們得到了欲證之不等式:
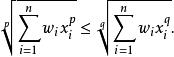 冪平均
冪平均最後使用先前證過的等價性,我們得到了關於負數 p與 q的不等式,證畢。
推廣
冪平均可以推廣到更一般的廣義 f-平均:
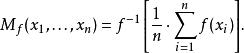 冪平均
冪平均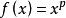 冪平均
冪平均例如這包括了幾何平均而勿需使用極限。冪平均是由得到的。
套用
信號處理
冪平均作為一個非線性移動平均。對於小p 值,冪平均比較偏重小信號值,對於大 p 值,冪平均則會強調大信號值。對於大 p 值,這可作為一個整流信號的包封檢測器(envelope detector)。對於小 p值,這可作為一個質量譜的基線偵測器(baseline detector)。