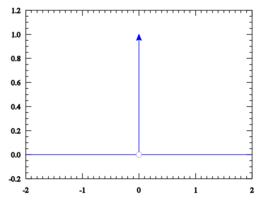
定義
物理學中常常要研究一個物理量在空間或時間中分布的密度,例如質量密度、電荷密度、每單位時間傳遞的動量(即力)等等,但是物理學中又常用到質點、點電荷、瞬時力等抽象模型,他們不是連續分布於空間或時間中,而是集中在空間中的某一點或者時間中的某一瞬時,那么它們的密度應該如何表示呢?
一種定義
為了在數學上理想地表示出這種密度分布,引入了δ函式的概念。用數學表示為:
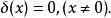 狄拉克δ函式
狄拉克δ函式 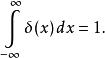 狄拉克δ函式
狄拉克δ函式 上述表達式不規定δ函式在0點的取值,是因為這個值無法嚴謹地表述出來,不能籠統的定義為正無窮,並且函式取值的“大小”是由第二個積分式決定的,因此只需限定取值為零的區域即可 。如果函式不在0點取非零值,而在其他地方,可定義
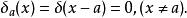 狄拉克δ函式
狄拉克δ函式 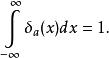 狄拉克δ函式
狄拉克δ函式 另一種定義
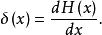 狄拉克δ函式
狄拉克δ函式 其中H(x)稱為階躍函式或亥維賽單位函式:
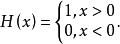 狄拉克δ函式
狄拉克δ函式 可以證明兩種定義是等價的。從第二個定義中,可以看到δ函式可以通過對階躍函式取微分得到,實際上,只要我們對一個不連續函式取微分,就會出現δ函式 。
理解
嚴格來說δ函式不能算是一個函式,因為滿足以上條件的函式是不存在的。數學上,人們為這類函式引入了廣義函式的概念,在廣義函式的理論中, δ函式的確切意義應該是在積分意義下來理解。在實際套用中, δ函式總是伴隨著積分一起出現 。δ分布在偏微分方程、數學物理方法、傅立葉分析和機率論里都有很重要的套用。
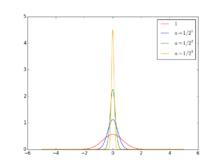 圖1.高斯分布函式a趨近於0的序列
圖1.高斯分布函式a趨近於0的序列 一些函式可以認為是狄拉克δ函式的近似,但是要注意,這些函式都是通過極限構造的,因此嚴格上都不是狄拉克δ函式本身,不過在一些數學計算中可以作為狄拉克δ函式進行計算。
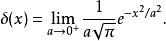 狄拉克δ函式
狄拉克δ函式 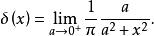 狄拉克δ函式
狄拉克δ函式 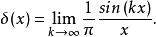 狄拉克δ函式
狄拉克δ函式 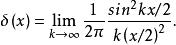 狄拉克δ函式
狄拉克δ函式 性質
狄拉克δ函式有以下性質 ,在理解這些性質的時候,應該認為等式兩邊分別作為被積函式的因子時得到的結果相等。
對稱性
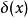 狄拉克δ函式
狄拉克δ函式 偶函式,其導數是奇函式
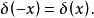 狄拉克δ函式
狄拉克δ函式 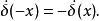 狄拉克δ函式
狄拉克δ函式 放縮
放縮(或相似性)
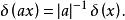 狄拉克δ函式
狄拉克δ函式 挑選性
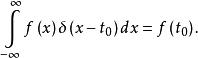 狄拉克δ函式
狄拉克δ函式 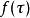 狄拉克δ函式
狄拉克δ函式 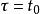 狄拉克δ函式
狄拉克δ函式 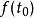 狄拉克δ函式
狄拉克δ函式 這種性質稱為挑選性,它將 在 點的值 挑選出來
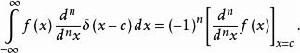 狄拉克δ函式
狄拉克δ函式 上述性質則可看成適用於高階導數的挑選性。
方程的解
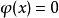 狄拉克δ函式
狄拉克δ函式 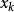 狄拉克δ函式
狄拉克δ函式 如果方程 的實根 全是單根,則
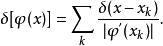 狄拉克δ函式
狄拉克δ函式 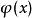 狄拉克δ函式
狄拉克δ函式 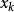 狄拉克δ函式
狄拉克δ函式 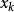 狄拉克δ函式
狄拉克δ函式 該等式的含義為,若將δ函式作用在一個函式上,則會把函式的實根挑選出來,其左邊表示在函式 為零時會取非零值,右邊表示在 處,會取得非零值,並且取值“大小”,或者說在積分中的作用大小與δ函式的比值是函式在 處導數的絕對值的倒數。通過這一性質可以得到一些具體的等式,如
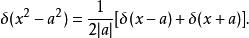 狄拉克δ函式
狄拉克δ函式 與x乘積
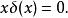 狄拉克δ函式
狄拉克δ函式 以及
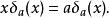 狄拉克δ函式
狄拉克δ函式 這個性質說明δ函式與x的乘積在積分中與0的作用是相同的。
分母為零
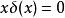 狄拉克δ函式
狄拉克δ函式 方程 表明,當我們用x去除方程的兩邊,並且x可以取為零時,我們應該在其中一邊加上δ函式的某個倍數 ,即我們從方程
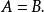 狄拉克δ函式
狄拉克δ函式 不能推斷出
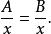 狄拉克δ函式
狄拉克δ函式 只能推斷出
 狄拉克δ函式
狄拉克δ函式 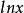 狄拉克δ函式
狄拉克δ函式 研究函式 的微分,一般的公式是
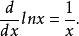 狄拉克δ函式
狄拉克δ函式 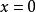 狄拉克δ函式
狄拉克δ函式 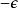 狄拉克δ函式
狄拉克δ函式  狄拉克δ函式
狄拉克δ函式  狄拉克δ函式
狄拉克δ函式 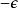 狄拉克δ函式
狄拉克δ函式  狄拉克δ函式
狄拉克δ函式 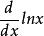 狄拉克δ函式
狄拉克δ函式 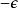 狄拉克δ函式
狄拉克δ函式  狄拉克δ函式
狄拉克δ函式 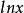 狄拉克δ函式
狄拉克δ函式  狄拉克δ函式
狄拉克δ函式 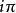 狄拉克δ函式
狄拉克δ函式 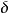 狄拉克δ函式
狄拉克δ函式 為了使導函式在 附近是有明確定義(非正常函式的意義)的,通常會對它加上一個附加條件,即它從 到 的積分為0,而上式中 從 到 的積分為零, 從 到 的積分卻是-iπ,因此上式就不是一個正確的等式了,為了改正它,需要增加一個修正項,我們注意到 在 的負值處有一個虛數項 ,這個項在0附近有一個突變,對它微分會產生一個 函式,那么等式變成
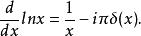 狄拉克δ函式
狄拉克δ函式 傅立葉變換
δ函式的傅立葉變換是,
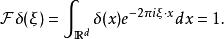 狄拉克δ函式
狄拉克δ函式 根據δ函式的定義,δ函式並不是通常意義下的一般函式,應當看作一種函式列的極限或者泛函,因此δ函式的傅立葉積分也不是通常意義的傅立葉積分而是一種廣義的傅立葉積分。
可見,δ函式與常數1是一對傅立葉變換的共軛函式。
δ函式的傅立葉逆變換是:
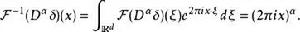 狄拉克δ函式
狄拉克δ函式 多維δ函式
定義
在多維空間中的δ函式定義如下
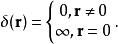 狄拉克δ函式
狄拉克δ函式 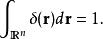 狄拉克δ函式
狄拉克δ函式 例如在三維空間中,三維δ函式可表示為三個一維δ函式乘積表示,在直角坐標系中
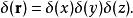 狄拉克δ函式
狄拉克δ函式 在極坐標系中
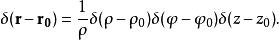 狄拉克δ函式
狄拉克δ函式 在球坐標系中
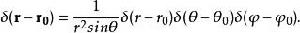 狄拉克δ函式
狄拉克δ函式 性質
多維的δ函式主要性質
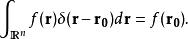 狄拉克δ函式
狄拉克δ函式 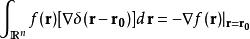 狄拉克δ函式
狄拉克δ函式 位矢的微分
δ函式可以表示如下 :
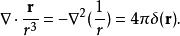 狄拉克δ函式
狄拉克δ函式 套用
靜電場
點電荷等抽象模型的密度分布可以表示為
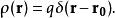 狄拉克δ函式
狄拉克δ函式 一組點電荷的電荷密度可以表示為
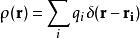 狄拉克δ函式
狄拉克δ函式 不僅可以用δ函式表示點電荷的密度分布,還可以表示圓柱、球殼上的電荷密度。例如,在電荷q均勻分布在半徑為a的球上,在球坐標系中其電荷密度為
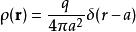 狄拉克δ函式
狄拉克δ函式 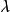 狄拉克δ函式
狄拉克δ函式 在半徑為b的圓柱上均勻分布的電荷單位長度的電荷為 ,在柱坐標系中其電荷密度為
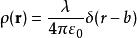 狄拉克δ函式
狄拉克δ函式 電學的高斯定理微分形式為
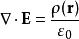 狄拉克δ函式
狄拉克δ函式 電場強度為
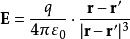 狄拉克δ函式
狄拉克δ函式 因此位矢的微分可以表示成
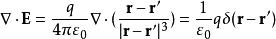 狄拉克δ函式
狄拉克δ函式 也可代入電荷密度的表達式直接得到 。
結構力學
在結構力學中, δ函式可以用來描述結構上的瞬時荷載或點荷載。一個諧振子在 t=0時突然受到衝量為 I的力的衝擊,其演變可以如下描述:
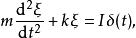 狄拉克δ函式
狄拉克δ函式 其中 m是質量,ξ是撓度,而 k是彈簧常數。
δ測度
測度論中
在測度論中,與δ函式相應的有δ測度,其定義如下
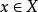 狄拉克δ函式
狄拉克δ函式 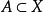 狄拉克δ函式
狄拉克δ函式 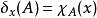 狄拉克δ函式
狄拉克δ函式 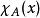 狄拉克δ函式
狄拉克δ函式 設X是一個非空集,任意選取元素 ,對任意集合 ,定義 其中 為集合A的特徵函式,定義為
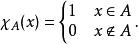 狄拉克δ函式
狄拉克δ函式 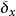 狄拉克δ函式
狄拉克δ函式 稱 為元素x處的δ測度。
構造
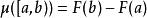 狄拉克δ函式
狄拉克δ函式 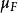 狄拉克δ函式
狄拉克δ函式 Lebesgue-Stieltjes測度定義為:設F(x)是實數R上單增右連續的函式,對於區間[a,b),定義 為(R,F)上的Lebesgue-Stieltjes測度,記為 。
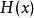 狄拉克δ函式
狄拉克δ函式 則δ測度可表示為階躍函式 的Lebesgue-Stieltjes測度,即
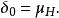 狄拉克δ函式
狄拉克δ函式 計數測度
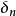 狄拉克δ函式
狄拉克δ函式 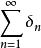 狄拉克δ函式
狄拉克δ函式 記 為n點(n為整數)處的δ測度,則 恰是整數集N上的計數測度。