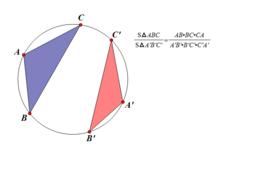
證明
情況1
共圓定理兩個三角形在同圓中：（證法見右圖）
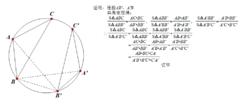
情況2
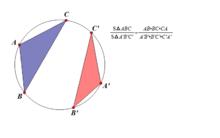共圓定理兩個三角形在等圓中：只需將兩個等圓平移至重合，轉換為同圓中的情況
套用
共圓定理雖然十分簡潔，但它的用處不小，尤其是在面積法解題的過程中，發揮著巨大的作用
用面積法證明蝴蝶定理
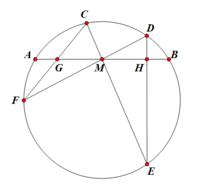蝴蝶定理蝴蝶定理：AB是圓內的一段弦，M是AB中點，C、D是圓上的任意兩點，連線CM、DM並延長分別交圓於E、F，連線DE、CF分別交AB於G、H，則MG=MH（見右上圖）
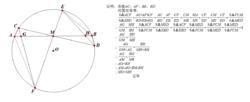用面積法證明蝴蝶定理（證明過程見右下圖）
用面積法證明坎迪定理
坎迪定理：AB是圓內的一段弦，P是弦AB上任意一點，C、D是圓上的任意兩點，連線CP、DP並延長分別交圓於E、F，連線DE、CF分別交AB於G、H，設AP=a，BP=b，GP=x，HP=y，則(1/a)-(1/b)=(1/x)-(1/y)
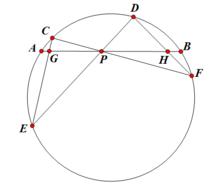坎迪定理（見右上圖）【PS：坎迪定理是蝴蝶定理的一般形式】
用面積法證明坎迪定理（證明過程見右下圖）
PS：共圓定理還可以證明蝴蝶定理和坎迪定理的一些推廣
用於導比例
共圓定理可以用於導比例，比如下面一道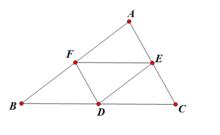例題
例題在三角形ABC中，D、E、F分別是線段BC、線段AC、線段AB上的點，連線DE、EF、DF，且DE=1/2AB，DF=1/2AC，EF=1/2BC，求證：D、E、F分別是BC、AC、AB中點（見右上圖）
例題證明（證明過程見右下圖）
PS：共圓定理還有其他的套用，在此就不一一列舉了
