基本介紹
三角形中的米奎爾定理(Miquel)定理和其推論在處理平面幾何中的有關問題,特別是有關競賽題時,常發揮重要作用。
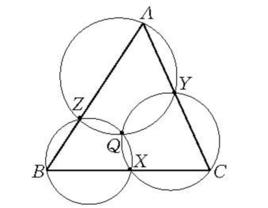
定理(米奎爾定理) 設在一個三角形每邊所在直線上取一點,過三角形的每一個頂點與兩條鄰邊所線上上所取的點作圓,則這三個圓交於一點,則該點稱為“米奎爾點”。
利用圓周角性質易證此定理 。
米奎爾定理的推論
當上述三點共線時,可得如下推論。
推論1
(完全四邊形的密克定理) 四條兩兩相交的直線形成四個三角形,它們的外接圓共點 。
推論2
在△ABC中,點D、E、F分別在邊BC、CA、AB上,設M為其米奎爾點,當AD⊥BC,且M在直線AD上時,點E、F與△BDF,△DCE的外心O₁、O₂四點共圓的充分必要條件是M為△ABC的垂心。
推論2的證明 如圖1。
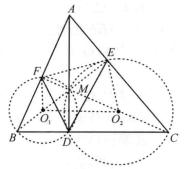 圖1
圖1由∠MEC=180°-∠MDC=90°,知ME⊥AC,同理,MF⊥AB。
由AF·AB=AM·AD=AE·AC,知B、C、E、F四點共圓,又AD⊥BC,則O₁、O₂分別為BM、CM的中點,即有O₁O₂ // BC,從而,∠MO₂O₁=∠MCB。
充分性 當M為△ABC的垂心時,由九點圓定理即知O₁、O₂、E、F四點共圓。
必要性 當O₁、O₂、E、F四點共圓時,有∠O₁O₂E+∠EFO₁= 180°。
由B、C、E、F四點共圓有∠BFE+2∠BCE= 180°。
設R為△ABC的外接圓半徑,故
 米奎爾定理
米奎爾定理 米奎爾定理
米奎爾定理∠ABM=∠MCARt△BMF∽Rt△CMEMF/BF= ME/CE
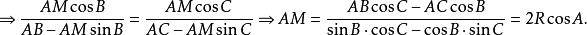 米奎爾定理
米奎爾定理推論3
在完全四邊形ABCDEF中,設M為其米奎爾點,則
(1)當A、B、D、F四點共圓於⊙O時,M在直線CE上,且OM⊥CE;
(2)當B,C,E,F四點共圓於⊙O時,M在直線AD上,且 OM⊥AD。
推論3的證明:
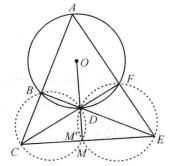 圖2
圖2(1)如圖2,設△BCD的外接圓與CE交於點M',聯結DM'。則∠DM'C=∠ABD=∠DFE,即知E、F、D、M'四點共圓。從而,M'為完全四邊形的密克點。故點M'與M重合。設⊙O的半徑為R,則CM·CE=CD·CF=CO²-R²。
同理,EM·EC= EO²-R²。
故CO²-EO²=EC(CM-EM)= (CM+ EM)(CM- EM)= CM²-EM²。
由定差冪線定理知OM⊥CE
(2)類似可證 。
套用舉例
【例1】在銳角△ABC中,AB<AC,AD是邊BC上的高,P是線段AD內一點,過P作PE⊥AC,垂足為E,作PF⊥AB,垂足為F,O₁、O₂分別是△BDF、△CDE的外心。證明:O₁、O₂、E、F四點共圓的充分必要條件為P是△ABC的垂心。
(2007,全國高中數學聯合競賽)事實上,由推論2即證 。
【例2】已知△ABC的內切圓分別切三邊BC、CA、AB於點D、E、F,△ABC的外接圓⊙O與△AEF的外接圓⊙O₁、△BFD的外接圓⊙O₂、△CDE的外接圓⊙O₃分別交於點A和P、B和Q、C和R。證明:
(1)⊙O₁、⊙O₂、⊙O₃交於一點;
(2)PD、QE、RF三線交於一點。
(第39屆加拿大數學奧林匹克)
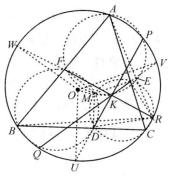 圖3
圖3證明:(1)如圖,顯然,⊙O₁、⊙O₂、⊙O₃均過△ABC的內心。
(2)如圖,聯結RE、RD、RA、RB,則
∠ERD=∠ECD=∠ACB=∠ARB,
從而,∠ARE=∠BRD,
又∠RAC=∠RBC,得△ARE∽△BRD。
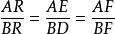 米奎爾定理
米奎爾定理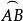 米奎爾定理
米奎爾定理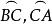 米奎爾定理
米奎爾定理故,即RF平分∠ARB,因此,RF過⊙O的弧的中點W,同理,PD、QE分別過⊙O上弧的中點U,V。
下面證明:DU、EV、FW三線交於一點,
由MD⊥BC,OU⊥BC,知MD // OU。同理,ME// OV,MF// OW。
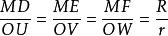 米奎爾定理
米奎爾定理設△ABC的外接圓,內切圓半徑分別為R、r,則。若設直線OM與
UD交於點K,則由上述比例式,知直線VE、WF均過點K,故直線PD、QE、RF三線共點於K 。