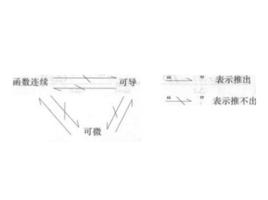
定義
設z是u、v的二元函式z=f(u,v)，u、v是x的一元函式u=u(x)、v=v(x)，z通過中間變數u、v構成自變數x的複合函式。這種兩個中間變數、一個自變數的多元複合函式是一元函式，其導數稱為全導數。
相關定理
一一型鎖鏈法則
在中間變數只有一個時，如z=f(u,x)，它在相應點有連續導數，則可得一一型全導數鎖鏈法則，即：
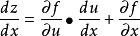全導數二一型鎖鏈法則
設u=u(x)、v=v(x)在x可導，z=f(u,v)在相應點(u,v)有連續偏導數，則複合函式z=f(u(x),v(x))在x可導，且有：
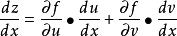全導數證明：對於自變數x的該變數△x，變數u=u(x)、v=v(x)的改變數△u,△v，進一步有函式的該變數△z，因為函式z=f(u,v)可微，即有
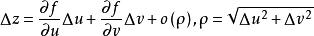全導數對上式左右兩端同除△x，得到：
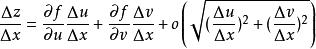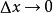全導數
全導數又因為u=u(x)、v=v(x)可導，當時，對上式左右兩端同時取極限，則有：
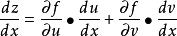全導數至此，證明完畢。
三一型鎖鏈法則
在中間變數多於兩個時，如z=f(u,v,w)，而u=u(x)、v=v(x)、w=w(x)，類似可得三一型全導數鎖鏈法則，即：
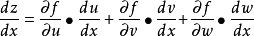全導數典例
例1
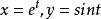全導數z=f(x,y)有連續的偏導數，，求複合函式的全導數。
解：由二一型全導數鎖鏈法則，計算得到：
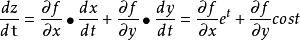全導數例2
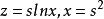全導數，求複合函式的全導數。
解：外層函式顯含自變數s，由一一型全導數鎖鏈法則，計算得到：
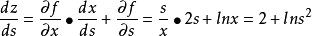全導數