方嚮導數
導數
 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度定義 設函式 在點 的某領域內有定義,若極限
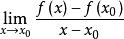 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度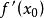 方嚮導數與梯度
方嚮導數與梯度存在,則稱函式 在點 處可導,並稱該極限為函式 在點 處的導數,記作 。
定義
 方嚮導數與梯度
方嚮導數與梯度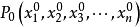 方嚮導數與梯度
方嚮導數與梯度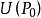 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度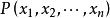 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度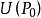 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度設三元函式 在點 的某領域 在 中有定義, 為從點 出發的射線, 為 上且含於 內的任一點,以ρ表示 與 兩點間的距離。若極限
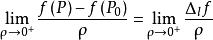 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度存在,則稱此極限為函式 在點 沿方向 的方嚮導數 ,記作
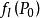 方嚮導數與梯度
方嚮導數與梯度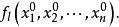 方嚮導數與梯度
方嚮導數與梯度或
方嚮導數與偏導數、全微分的關係
 方嚮導數與梯度
方嚮導數與梯度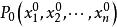 方嚮導數與梯度
方嚮導數與梯度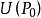 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度定理1 多元函式 在點 的某個領域 在 中有定義,且在點 處可微,則在該點處 任意方向上的方嚮導數都存在,但反之不成立 。
 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度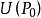 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度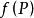 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度證:設向量 為從 出發的射線,為 上且含於 內的任一點,並以ρ表示 與 兩點間的距離,由假設知多元函式 點 處可微,從而有:
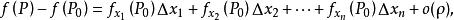 方嚮導數與梯度
方嚮導數與梯度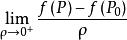 方嚮導數與梯度
方嚮導數與梯度也即有存在,按照定義即證明了方嚮導數存在,且
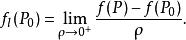 方嚮導數與梯度
方嚮導數與梯度梯度
定義
 方嚮導數與梯度
方嚮導數與梯度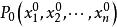 方嚮導數與梯度
方嚮導數與梯度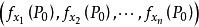 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度若多元函式在點存在對所有自變數的偏導數,則稱向量為函式在點的梯度 ,記作
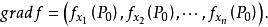 方嚮導數與梯度
方嚮導數與梯度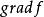 方嚮導數與梯度
方嚮導數與梯度向量的長度(或模)為
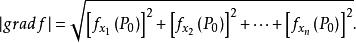 方嚮導數與梯度
方嚮導數與梯度梯度與方嚮導數的關係
 方嚮導數與梯度
方嚮導數與梯度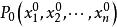 方嚮導數與梯度
方嚮導數與梯度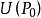 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度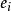 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度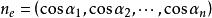 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度定理2 設多元函式
在點的某個領域屬於內有定義,且在點處可微。其中是軸對應的單位向量。向量為向量的方向餘弦。則有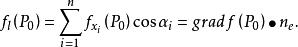 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度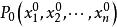 方嚮導數與梯度
方嚮導數與梯度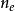 方嚮導數與梯度
方嚮導數與梯度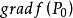 方嚮導數與梯度
方嚮導數與梯度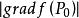 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度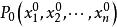 方嚮導數與梯度
方嚮導數與梯度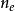 方嚮導數與梯度
方嚮導數與梯度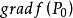 方嚮導數與梯度
方嚮導數與梯度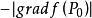 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度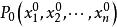 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度註:若多元函式在點點可微,當與方向相同時,方嚮導數取得最大值,也即在得梯度方向是其增長最快方向;當與方向相反時,方嚮導數取得最小值,也即在的梯度反方向是的值減少最快方向。
套用
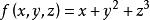 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度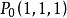 方嚮導數與梯度
方嚮導數與梯度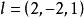 方嚮導數與梯度
方嚮導數與梯度(1)設,求在點沿方向的方嚮導數。
 方嚮導數與梯度
方嚮導數與梯度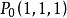 方嚮導數與梯度
方嚮導數與梯度解:易見在點可微。所以
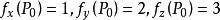 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度以及方向的方向餘弦
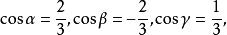 方嚮導數與梯度
方嚮導數與梯度故
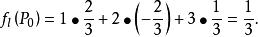 方嚮導數與梯度
方嚮導數與梯度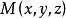 方嚮導數與梯度
方嚮導數與梯度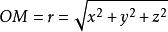 方嚮導數與梯度
方嚮導數與梯度 方嚮導數與梯度
方嚮導數與梯度(2)設質量為m的質點位於原點,質量為1的質點位於,記,求的梯度。
解:
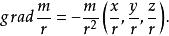 方嚮導數與梯度
方嚮導數與梯度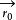 方嚮導數與梯度
方嚮導數與梯度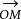 方嚮導數與梯度
方嚮導數與梯度若以表示上的單位向量,則有
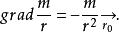 方嚮導數與梯度
方嚮導數與梯度