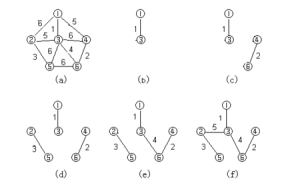
基本思想
先構造一個只含 n 個頂點、而邊集為空的子圖,把子圖中各個頂點看成各棵樹上的根結點,之後,從網的邊集 E 中選取一條權值最小的邊,若該條邊的兩個頂點分屬不同的樹,則將其加入子圖,即把兩棵樹合成一棵樹,反之,若該條邊的兩個頂點已落在同一棵樹上,則不可取,而應該取下一條權值最小的邊再試之。依次類推,直到森林中只有一棵樹,也即子圖中含有 n-1 條邊為止。
步驟
新建圖G,G中擁有原圖中相同的節點,但沒有邊;
將原圖中所有的邊按權值從小到大排序;
從權值最小的邊開始,如果這條邊連線的兩個節點於圖G中不在同一個連通分量中,則添加這條邊到圖G中;
重複3,直至圖G中所有的節點都在同一個連通分量中。
1.新建圖G,G中擁有原圖中相同的節點,但沒有邊;
2.將原圖中所有的邊按權值從小到大排序;
3.從權值最小的邊開始,如果這條邊連線的兩個節點於圖G中不在同一個連通分量中,則添加這條邊到圖G中;
4.重複3,直至圖G中所有的節點都在同一個連通分量中。
證明
這樣的步驟保證了選取的每條邊都是橋,因此圖G構成一個樹。
為什麼這一定是最小生成樹呢?關鍵還是步驟3中對邊的選取。算法中總共選取了n-1條邊,每條邊在選取的當時,都是連線兩個不同的連通分量的權值最小的邊
要證明這條邊一定屬於最小生成樹,可以用反證法:如果這條邊不在最小生成樹中,它連線的兩個連通分量最終還是要連起來的,通過其他的連法,那么另一種連法與這條邊一定構成了環,而環中一定有一條權值大於這條邊的邊,用這條邊將其替換掉,圖仍舊保持連通,但總權值減小了。也就是說,如果不選取這條邊,最後構成的生成樹的總權值一定不會是最小的。
1.這樣的步驟保證了選取的每條邊都是橋,因此圖G構成一個樹。
2.為什麼這一定是最小生成樹呢?關鍵還是步驟3中對邊的選取。算法中總共選取了n-1條邊,每條邊在選取的當時,都是連線兩個不同的連通分量的權值最小的邊
3.要證明這條邊一定屬於最小生成樹,可以用反證法:如果這條邊不在最小生成樹中,它連線的兩個連通分量最終還是要連起來的,通過其他的連法,那么另一種連法與這條邊一定構成了環,而環中一定有一條權值大於這條邊的邊,用這條邊將其替換掉,圖仍舊保持連通,但總權值減小了。也就是說,如果不選取這條邊,最後構成的生成樹的總權值一定不會是最小的。
時間複雜度
平均時間複雜度為O(|E|log|E|),其中E和V分別是圖的邊集和點集。