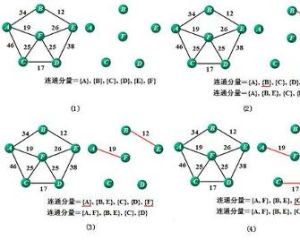
算法定義
克魯斯卡爾算法
假設 WN=(V,{E}) 是一個含有 n 個頂點的連通網,則按照克魯斯卡爾算法構造最小生成樹的過程為:先構造一個只含 n 個頂點,而邊集為空的子圖,若將該子圖中各個頂點看成是各棵樹上的根結點,則它是一個含有 n 棵樹的一個森林。之後,從網的邊集 E 中選取一條權值最小的邊,若該條邊的兩個頂點分屬不同的樹,則將其加入子圖,也就是說,將這兩個頂點分別所在的兩棵樹合成一棵樹;反之,若該條邊的兩個頂點已落在同一棵樹上,則不可取,而應該取下一條權值最小的邊再試之。依次類推,直至森林中只有一棵樹,也即子圖中含有 n-1條邊為止。
舉例描述
克魯斯卡爾算法(Kruskal's algorithm)是兩個經典的最小生成樹算法的較為簡單理解的一個。這裡面充分體現了貪心算法的精髓。大致的流程可以用一個圖來表示。這裡的圖的選擇借用了Wikipedia上的那個。非常清晰且直觀。
首先第一步,我們有一張圖,有若干點和邊
第一步我們要做的事情就是將所有的邊的長度排序,用排序的結果作為我們選擇邊的依據。這裡再次體現了貪心算法的思想。資源排序,對局部最優的資源進行選擇。
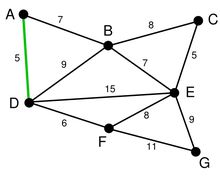
排序完成後,我們率先選擇了邊AD。這樣我們的圖就變成了
 kruskal算法
kruskal算法.
.
.
.
.
.
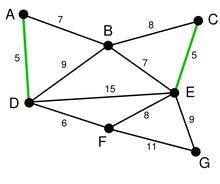
第二步,在剩下的邊中尋找。我們找到了CE。這裡邊的權重也是5
 kruskal算法
kruskal算法.
.
.
.
.
.
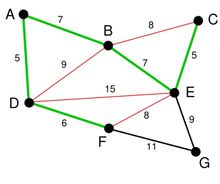
依次類推我們找到了6,7,7。完成之後,圖變成了這個樣子。
 kruskal算法
kruskal算法.
.
.
.
.
.
下一步就是關鍵了。下面選擇那條邊呢? BC或者EF嗎?都不是,儘管現在長度為8的邊是最小的未選擇的邊。但是他們已經連通了(對於BC可以通過CE,EB來連線,類似的EF可以通過EB,BA,AD,DF來接連)。所以我們不需要選擇他們。類似的BD也已經連通了(這裡上圖的連通線用紅色表示了)。
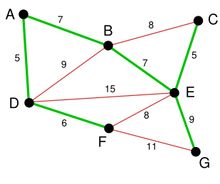
最後就剩下EG和FG了。當然我們選擇了EG。最後成功的圖就是下圖:
 kruskal算法
kruskal算法.
.
.
.
.
.
到這裡所有的邊點都已經連通了,一個最小生成樹構建完成。
Kruskal算法的時間複雜度由排序算法決定,若採用快排則時間複雜度為O(N log N)。
代碼實現
偽代碼
MST-KRUSKAL(G,
C
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | #include"stdio.h" #include"stdlib.h" structedge { intm; intn; intd; }a[5010]; int cmp (const void *a,constvoid*b)//按升序排列 { return((structedge*)a)->d>((structedge*)b)->d; } intmain(void) { inti,n,t, num ,min,k,g,x[100]; printf("請輸入頂點的個數:"); scanf ("%d",&n); t=n*(n-1)/2; for(i=1;i<=n;i++) x[i]=i; printf("請輸入每條邊的起始端點、 權值 :/n"); for(i=0;i<t;i++) scanf("%d%d%d",&a[i].m,&a[i].n,&a[i].d);//輸入每條邊的權值 qsort (a,t,sizeof(a[0]),cmp); min=num=0; for(i=0;i<t&#<n-1;i++) { for(k=a[i].m;x[k]!=k;k=x[k])//判斷線段的起始點所在的集合 x[k]=x[x[k]]; for(g=a[i].n;x[g]!=g;g=x[g])//判斷線段的終點所在的集合 x[g]=x[x[g]]; if(k!=g)//如果線段的兩個端點所在的集合不一樣 { x[g]=k; min+=a[i].d; num++; printf(" 最小生成樹 中加入邊:%d%d/n",a[i].m,a[i].n); } } printf("最小生成樹的權值為:%d/n",min); system(" pause "); return0; } |
matlab
function Kruskal(w,MAX)
%此程式為最小支撐樹的Kruskal算法實現
%w為無向圖的距離矩陣,
%MAX為距離矩陣中∞的實際輸入值
%時間:2011年6月22日0:07:53
len=length(w); %圖的點數
edge=zeros(len*(len-1),3); %用於存儲圖中的邊
count=1; %圖中的邊數
for i=1:len-1 %循環距離矩陣,
for j=i+1:len
if w(i,j)~=MAX
edge(count,1)=w(i,j);
edge(count,2)=i;
edge(count,3)=j;
count=count+1;
end
end
end
edge=edge(1:count-1,:); %去掉無用邊
[tmp,index]=sort(edge(:,1)); %所有邊按升序排序
i=3; %其實測試邊數為3條(3條以下無法構成圈,
while 1
x=findcycle(edge(index(1:i),:),len); %檢測這些邊是否構成圈
if x
index(i)=0; %若構成圈,則將該邊對應的index項標記為0,
else
i=i+1; %若沒有構成圈,則i加1,
end
index=index(index>0); %將構成圈的邊從index中除去
if i==len
break; %找到符合條件的點數減一條的邊,
end
end
index=index(1:len-1); %截短index矩陣,
%%%%%%%%%%%% 結果顯示 %%%%%%%%%%%%%
s=sprintf('\n\t%s\t%s\t %s\t','邊端點','距離','是否在最小支撐樹');
for i=1:count-1
edge_tmp=edge(i,:);
if ~isempty(find(index==i,1))
s_tmp=sprintf('\n \t (%d,%d)\t %d\t %s\t',edge_tmp(2),edge_tmp(3),edge_tmp(1),'√');
else
s_tmp=sprintf('\n \t (%d,%d)\t %d\t %s\t',edge_tmp(2),edge_tmp(3),edge_tmp(1),'×');
end
s=strcat(s,s_tmp);
end
disp(s);
end
function isfind=findcycle(w,N)
%本程式用於判斷所給的邊能否構成圈:有圈,
%w:輸入的邊的矩陣
%N:原圖的點數
%原理:不斷除去出現次數小於2的端點所在的邊,
len=length(w(:,1));
index=1:len;
while 1
num=length(index); %邊數
p=zeros(1,N); %用於存儲各點的出現的次數(一條邊對應兩個端點)
for i=1:num %統計各點的出現次數
p(w(index(i),2))=p(w(index(i),2))+1;
p(w(index(i),3))=p(w(index(i),3))+1;
end
index_tmp=zeros(1,num); %記錄除去出現次數小於2的端點所在的邊的邊的下標集合
discard=find(p<2); %找到出現次數小於2的端點
count=0; %記錄剩餘的邊數
for i=1:num
%判斷各邊是否有僅出現一次端點——沒有,
if ~(~isempty(find(discard==w(index(i),2),1)) || ~isempty(find(discard==w(index(i),3),1)))
count=count+1;
index_tmp(count)=index(i);
end
end
if num==count %當沒有邊被被除去時,
index=index_tmp(1:count); %更新index
break;
else
index=index_tmp(1:count); %更新index
end
end
if isempty(index) %若最後剩下的邊數為0,
isfind=0;
else
isfind=1;
end
end
%
% a =[
% 0 3 2 3 100 100 100
% 3 0 2 100 100 100 6
% 2 2 0 3 100 1 100
% 3 100 3 0 5 100 100
% 100 100 100 5 0 4 6
% 100 100 1 100 4 0 5
% 100 6 100 6 100 5 0];
%
% Kruskal(a,100)
pascal
{
最小生成樹的Kruskal算法。
Kruskal算法基本思想:
每次選不屬於同一連通分量(保證不生成圈)且邊權值最小的頂點,將邊加入MST,並將所在的2個連通分量合併,
排序使用Quicksort(O(eloge))
檢查是否在同一連通分量用Union-Find,
Union-Find使用rank啟發式合併和路徑壓縮
總複雜度O(eloge)=O(elogv) (因為e
}
const
maxn=100;
maxe=maxn*maxn;
type
edge=record
a,b :integer; //邊的2個頂點
len :integer; //邊的長度
end;
var
edges :array[0..maxe]of edge; //保存所有邊的信息
p,r :array[0..maxn]of integer; //p保存i的父親節點,
n,e :integer; //n為頂點數,
procedure swap(a,b:integer); //交換
begin
edges:=edges[a];
edges[a]:=edges[b];
edges[b]:=edges;
end;
procedure quicksort(l,r:integer); //快速排序
var
x,i,j :integer;
begin
x:=edges[random(r-l+1)+l].len;
i:=l;j:=r;
repeat
while edges[i].leninc(i);
while edges[j].len>x do dec(j);
if i<=j then
begin
swap(i,j);
inc(i);dec(j);
end
until i>j;
if l
if i
end;
procedure init;
var
i :integer;
begin
assign(input,'g.ini');reset(input);
readln(n,e);
for i:=1 to e do readln(edges[i].a,edges[i].b,edges[i].len); //從檔案讀入圖的信息
for i:=1 to n do p[i]:=i; //初始化並查集
randomize;
quicksort(1,e); //使用快速排序將邊按權值從小到大排列
end;
function find(x:integer):integer; //並查集的Find,
begin
if x<>p[x] then p[x]:=find(p[x]);
find:=p[x]
end;
procedure union(a,b:integer); //如果不屬於且權值最小則將2個頂點合併到一個連通分量
var
t :integer;
begin
a:=find(a);b:=find(b);
if r[a]>r[b] then begin t:=a;a:=b;b:=t end;
if r[a]=r[b]then inc(r[a]);
p[a]:=b;
end;
procedure kruskal; //主過程
var
en :integer; //en為當前邊的編號
count :integer; //統計進行了幾次合併。
tot :integer; //統計最小生成樹的邊權總和
begin
count:=0;en:=0; tot:=0;
while count
begin
inc(en);
with edges[en] do
begin
if find(a)<>find(b) then
begin
union(a,b);
writeln(a,'--',b,':',len);
inc(tot,len);
inc(count);
end;
end;
end;
writeln('Total Length=",tot)
end;
{===========main==========}
begin
init;
kruskal;
end.
例題詳見 vijos p1045 Kerry 的電纜網路
type
rec=record
x,y:longint;
cost:real;
end;
var
f:array[1..1000000] of rec;
s,ans:real;
i,n,m,k,dad:longint;
father:array[1..1000000] of longint;
procedure kp(l,r:longint);
var
i,j:longint;
xx:real;
y:rec;
begin
i:=l;
j:=r;
xx:=f[(i+j) div 2].cost;
repeat
while xx>f[i].cost do inc(i);
while xx
if i<=j then
begin
y:=f[i];
f[i]:=f[j];
f[j]:=y;
inc(i);
dec(j);
end;
until i>j;
if i
if l
end;
function find(x:longint):longint;
begin
if father[x]=x then exit(x);
father[x]:=find(father[x]);
exit(father[x]);
end;
procedure union(x,y:longint;j:real);
begin
x:=find(x);
y:=find(y);
if x<>y then
begin
father[y]:=x;
ans:=ans+j;
inc(k);
end;
end;
begin
readln(s);
readln(n);
m:=0;
while not eof do
begin
inc(m);
with f[m] do
readln(x,y,cost);
end;
if m
begin
writeln("Impossible');
exit;
end;
for i:=1 to n do
father[i]:=i;
kp(1,m);
k:=0;
for i:=1 to m do
begin
if k=n-1 then break;
union(f[i].x,f[i].y,f[i].cost);
end;
if k
begin
writeln('Impossible');
exit;
end;
if ans>s then writeln('Impossible') else
writeln('Need ',ans:0:2,' miles of cable');
end.
Kruskal算法適用於邊稀疏的情形,
其它最小生成樹算法
c++
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | //本程式用到了並查集的基本操作,不會並查集的請自行學習或參考本代碼學習 //get fa 為查詢祖先,merge為將集合合併, same 是判斷兩個點是否處於同一集合 //getfa操作中使用了路徑壓縮即returnfa[x]=getfa(fa[x]),這樣可以減小並查集森林退化所帶來的 時間複雜度 #include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #defineMAXN_E100000 #defineMAXN_V100000 usingnamespacestd; structEdge{ intfm,to,dist; }e[MAXN_E]; intfa[MAXN_V],n,m; bool cmp (Edgea,Edgeb){ returna.dist<b.dist; } intgetfa(intx){//getfa是在並查集森林中找到x的祖先 if(fa[x]==x)returnfa[x]; elsereturnfa[x]=getfa(fa[x]); } intsame(intx,inty){ returngetfa(x)==getfa(y); } voidmerge(intx,inty){ int fax =getfa(x), fay =getfa(y); fa[fax]=fay; } intmain(){ scanf ("%d%d",&n,&m);//n為點數,m為邊數 for(inti=1;i<=m;i++) scanf("%d%d%d",&e[i] .fm ,&e[i].to,&e[i].dist);//用 邊集數組 存放邊,方便排序和調用 sort(e+1,e+m+1,cmp);//對邊按邊權進行升序排序 for(inti=1;i<=n;i++) fa[i]=i; intrst=n,ans=0;//rst表示目前的點共存在於多少個集合中,初始情況是每個點都在不同的集合中 for(inti=1;i<=m&&rst>1;i++) { intx=e[i].fm,y=e[i].to; if(same(x,y))continue;//same函式是查詢兩個點是否在同一集合中 else { merge(x,y);//merge函式用來將兩個點合併到同一集合中 rst--;//每次將兩個不同集合中的點合併,都將使rst值減1 ans+=e[i].dist;//這條邊是 最小生成樹 中的邊,將答案加上邊權 } } printf("%d\n",ans); return0; } |
java代碼實現
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 | importjava.util.ArrayList; importjava.util.Collections; classBianimplementsComparable//兩點之間的加權邊 { privateint first ,second;//表示一條邊的兩個節點 privateint value ;// 權值 publicBian(intfirst,intsecond,intvalue){ this.first=first; this.second=second; this.value=value; } publicintgetFirst(){ returnfirst; } publicintgetSecond(){ returnsecond; } publicintgetValue(){ returnvalue; } @Override publicintcompareTo(Objectarg0){ returnvalue>((Bian)arg0).value1 :(value==((Bian)arg0).value0:-1); } @Override publicStringtoString(){ return"Bian[first="+first+",second="+second+",value=" +value+"]"; } } classShuZu{ staticArrayList list =newArrayList();//存放每一個數組中的節點的數組 staticArrayList<ArrayList>bianList=newArrayList<ArrayList>();//對應存放數組中的邊的數組 publicstaticvoidcheck(Bianb)//檢查在哪個數組中 { if(list. size ()==0){ ArrayList sub =newArrayList(); sub. add (b.getFirst()); sub.add(b.getSecond()); list.add(sub); ArrayList<Bian>bian=newArrayList<Bian>(); bian.add(b); bianList.add(bian); return; } intfirst=b.getFirst(); intshuyu1=-1; intsecond=b.getSecond(); intshuyu2=-1; for(inti=0;i<list.size();i++)//檢查兩個節點分別屬於哪個數組 { for(intm=0;m<list.get(i).size();m++){ if(first==(Integer)list.get(i).get(m)) shuyu1=i; if(second==(Integer)list.get(i).get(m)) shuyu2=i; } } if(shuyu1==-1&&shuyu2==-1)//表示這兩個節點都沒有需要新加入 { ArrayList<Integer>sub=newArrayList<Integer>(); sub.add(b.getFirst()); sub.add(b.getSecond()); list.add(sub); ArrayList<Bian>bian=newArrayList<Bian>(); bian.add(b); bianList.add(bian); } if(shuyu1==-1&&shuyu2!=-1)//表示有一個點已經在數組中只把另一個加入就可以了 { list.get(shuyu2).add(first); bianList.get(shuyu2).add(b); } if(shuyu2==-1&&shuyu1!=-1)//表示有一個點已經在數組中只把另一個加入就可以了 { list.get(shuyu1).add(second); bianList.get(shuyu1).add(b); } if(shuyu1==shuyu2&&shuyu1!=-1)//表述兩個在同一個組中會形成環 { } if(shuyu1!=shuyu2&&shuyu1!=-1&&shuyu2!=-1)//表示兩個點在不同的組中需要合併 { for(inti=0;i<list.get(shuyu2).size();i++){ list.get(shuyu1).add(list.get(shuyu2).get(i)); } list.remove(shuyu2); for(inti=0;i<bianList.get(shuyu2).size();i++){ bianList.get(shuyu1).add(bianList.get(shuyu2).get(i)); } bianList.get(shuyu1).add(b); bianList.remove(shuyu2); } } publicstaticvoidshow(){ for(inti=0;i<bianList.get(0).size();i++) System.out.println(bianList.get(0).get(i)); } } publicclassTest{ publicstaticvoidmain(String[]args){ ArrayList<Bian>l=newArrayList<Bian>(); l.add(newBian(1,3,1)); l.add(newBian(1,2,6)); l.add(newBian(1,4,5)); l.add(newBian(2,3,5)); l.add(newBian(2,5,3)); l.add(newBian(3,4,5)); l.add(newBian(3,5,6)); l.add(newBian(3,6,4)); l.add(newBian(4,6,2)); l.add(newBian(5,6,6)); Collections.sort(l); //for(inti=0;i<l.size();i++) //System.out.println(l.get(i)); for(inti=0;i<l.size();i++) ShuZu.check(l.get(i)); ShuZu.show(); } } |