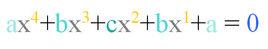釋義
1 如果一方程的根,兩兩互為倒數,或兩兩互為負倒數,則這樣的方程就叫倒數方程。
2 對於一元n次方程,將未知數的倒數1/x代替x,去分母整理後得到的方程如果與原方程相同,那么這樣的方程就叫倒數方程。
如x⁴+3x³+2x²+3x+1=0就是一個倒數方程。
標準形式
(該方程暫無特定標準形式)
方程特點
(1)倒數方程應為偶次方程(互為倒數的數成對出現)。
(2)倒數方程中各項係數關於中間項對稱。
(3)倒數方程沒有 x=0 的根。
(3)如果α是倒數方程的根,那么α的倒數1/α也是該方程的根。
變形推理
ax⁴+bx³+cx²+bx¹+a=0 (將未知數的倒數代替未知數)
↓
a(1/x)⁴+b(1/x)³+c(1/x)²+b(1/x)¹+a=0 (去分母:方程兩邊同時乘x⁴)
↓
a+bx¹+cx²+bx³+ax⁴=0 (整理:降次排列方程)
↓
ax⁴+bx³+cx²+bx¹+a=0 (得到與原方程相同的方程)
使用方法
例 若不等式ax +bx+c>0的解集為{x|α<x<β}(0<α<β),求cx +bx+a<0的解集.
解 ∵cx +bx+a=0是ax +bx+a=0的倒數方程.
且ax +bx+c>0解為α<x<β,
(解題說明:要在一題多解中鍛鍊自己的發散思維.)