2卵圓標準方程
卵圓的概念來自於禽鳥類的卵在平面上投影的形狀，習慣上稱作卵圓。具有一條對稱軸；三個參數；一頭大一頭小，兩頭不對稱，見示意圖1。
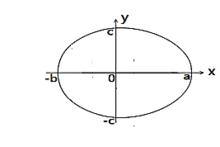卵圓標準方程圖1 卵圓示意圖是以x軸為對稱軸的卵圓標準方程 ：
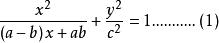卵圓標準方程（1）式中a、b、c為卵圓的參數，其中a稱做長半軸、b稱做短半軸、c稱做半寬。當a=b時便是橢圓方程，當a=b=c時便是圓方程。
卵圓圖形具有方向性，有四種相似標準方程，通過坐標旋轉可以得到另三種方程。
3方程推導
卵圓方程是基於橢圓（圓）的圖形特徵和方程性質，套用一元二次方程待定係數方法確定卵圓的方程係數。
3. 1 橢圓
3. 1.1圖形特徵
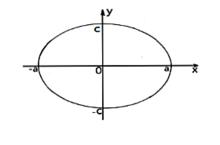卵圓標準方程圖2 橢圓示意圖
橢圓是對稱圖形，具有兩條對稱軸。為了便於對卵圓的描述，設：x軸為長=2a，y軸為寬=2c；x軸為對稱軸，y軸不限，反之亦然。由於x軸為對稱軸，y軸上寬的兩點看作是關於原點的對稱點。通過對橢圓圖形在x軸上進行擠壓或拉伸，使x軸上一邊的-a點移動到-b點，即a、-b兩點與原點不對稱，寬保持不變，生成類似於禽鳥類卵的形狀——卵圓，見圖1。
3. 1.2方程特性
根據橢圓知識，由圖2可知其標準方程：
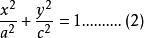卵圓標準方程橢圓標準方程的基本特性：一是沒有乘積項和一次項，是最簡單的二元二次方程；二是變數x和y的係數分別為橢圓特徵值（a、c）平方的倒數且相等；三是方程係數確定橢圓在坐標軸上點的位置。
3.2 係數待定法
橢圓的標準方程係數反映變數在坐標軸上兩個點的位置，坐標軸上的兩個點必然是方程的兩個解。對於長半軸為a的橢圓，當y=0時，由方程（2）得：
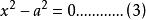卵圓標準方程
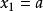卵圓標準方程
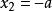卵圓標準方程式（3）屬於簡單的一元二次方程。一般情況能夠直接得出的兩個解： 、 。
代數中，兩個解的一元二次方程可以用因式分解乘積式方程表示：
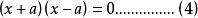卵圓標準方程式（3）和式（4）是等價的，只是表達方式不同。由於圖形變化，式（3）中係數參數也會發生相應變化，具有不確定性。式（4）屬於方程代數式，只與變形的結果相關，結果是確定的。可以利用式（4）確定變形後的方程係數，把這種方法稱為係數待定法。
係數待定的具體步驟：設卵圓標準方程變數x的對應係數為u的倒數，代入橢圓標準方程得標準卵圓方程：
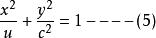卵圓標準方程
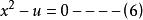卵圓標準方程當y=0 時，由方程（5）得：
設卵圓在x軸的點分別為：a、-b，則因式分解乘積式方程：
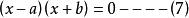卵圓標準方程令：方程（6）=（7），故：
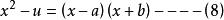卵圓標準方程
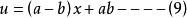卵圓標準方程化簡得：
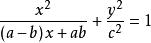卵圓標準方程將（9）代入（5）式得卵圓的標準方程：
4 基本 性質
卵圓曲線系複合函式方程，是以參數a、b和變數x相關的多項式為半軸與以c為半寬形成的不同橢圓的特定點的集合。
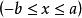卵圓標準方程橢圓的最大半軸為a，最小半軸為b，x取值範圍 。當x任取一值時，確定一個橢圓方程和在橢圓方程中對應點的y值，這個點也是卵圓曲線上的點。由於x是連續的，所以形成的點的集合屬於光滑曲線。
示例，設卵圓的三個參數為：a=5、b=4、c=3。首先，將參數代入式（1）得卵圓方程：
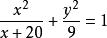卵圓標準方程
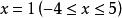卵圓標準方程其次，任取一值如 以，先只代入卵圓的方程係數，得特定的橢圓方程：
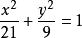卵圓標準方程然後，再以x=1代入特定的橢圓方程算得：y=2.9277。
x 、y的坐標（1，2.9277）點，既是橢圓上的點也是卵圓上的點。x的不同取值得到對應的y值,把得到的點光滑連線起來便是上述卵圓方程的曲線。
卵圓是具有一條對稱軸的圓。卵圓的寬偏離對稱軸的中點，並把對稱軸分成不相等的長、短兩個半軸；兩端不對稱一頭大一頭小，小頭為長半軸，大頭為短半軸。當對稱軸大於寬時屬於長型卵圓，寬大於對稱軸時屬於扁型卵圓。
卵圓是三參數圖形，長半軸以a表示、短半軸以b表示和半寬以c表示；三個參數必須大於0，參數之間相互獨立沒有隸屬關係；三個參數確定卵圓的形狀和大小。
長和寬的交點是卵圓的卵心，是確定卵圓的位置和圖形分析的參照點。卵圓沒有固定的焦點，不能形成動點與定點之間的固定關係。
作圖方法：一是電腦編程作圖，二是手工描點作圖。
參考文獻
[1] 劉紹學.數學2圓與方程[M].北京；人民教育出版社.2007；118-122.
[2] 劉紹學.數學選修2-1橢圓 [M].北京；人民教育出版社.2007；38-48.
