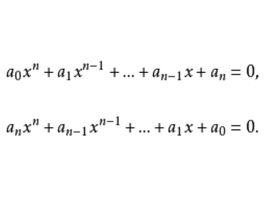倒根方程

倒根方程(reciprocal root equation)是指其根有特殊關係的兩個方程， 若一個一元n次方程的n個根都不為零，以這些根的倒數為根的方程叫作原方程的倒根方程 。

基本介紹

倒根方程即全部根相應互為倒數的兩個一元整式方程。如果x，x，…，x(均不為零)是一元n次方程ax +ax +…+ax+a=0(a≠0，a≠0)的n個根，那么以這n個根的倒數

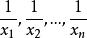倒根方程

為根的一元n次方程稱為原方程的倒根方程。把一元n次方程ax +ax +…+ax+a=0(a≠0，a≠0)的各項係數次序顛倒過來的方程ax +ax +…+ax+a=0(a≠0，a≠0)就和原方程互為倒根方程 。

相關介紹

定理 對於方程

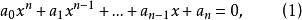倒根方程

其中a≠0，a≠0，則其倒根方程為

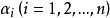倒根方程

倒根方程

略證：不妨設 為方程（1）的根，則得

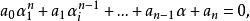倒根方程

兩邊同除

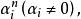倒根方程

便得

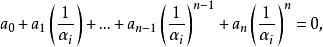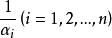倒根方程

倒根方程

即 為方程（2）的根。

同理可證，方程（2）的各根之倒數亦為方程（1）的根。從而證得方程（1）與方程②互為倒根方程。

我們可以利用這個定理較簡捷地求出某些一元刀次方程的各根 。

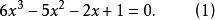倒根方程

【例】解方程

略解 ∵方程（1）的倒根方程

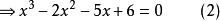倒根方程

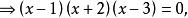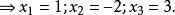倒根方程

倒根方程

由互為倒根方程的定理可得方程（1）的各根

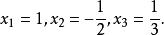倒根方程