概念
互反方程(reciprocal equation)是一種特殊的代數方程。數域P上的方程ax +ax +…+a=0 (a≠0)的係數若滿足a=a,a=a,…,則稱此方程為互反方程。當n為奇數時,x=-1是它的根;當n為偶數2m時,解此方程相當於解一個m次方程與一個二次方程。數域P上的方程是互反方程若且唯若它的倒數方程與該方程同解,即α為方程的根若且唯若1/α也為其根。
代數方程
指多項式方程,其一般形式為:
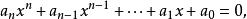 互反方程
互反方程是代數學中最基本的研究對象之一。
在20世紀以前,解方程一直是代數學的一個中心問題。二次方程的求解問題歷史久遠。在巴比倫泥板中(公元前18世紀)就載有二次方程的問題。古希臘人也解出了某些二次方程。中國古代數學家趙爽(公元3世紀)在求解一個有關面積的問題時,相當於給出二次方程的一個根。7世紀印度數學家婆羅摩笈多給出方程x +px-q=0的一個根的公式:
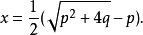 互反方程
互反方程一元二次方程的 一般解法是9世紀阿拉伯數學家花拉子米建立的。
對三次方程自古以來也有很多研究,在巴比倫泥板中,就有相當於三次方程的問題。阿基米德也曾討論過方程x +a=cx 的幾何解法。11世紀波斯數學家奧馬·海亞姆創立了用圓錐曲線解三次方程的幾何方法,他的工作可以看作是代數與幾何相結合的最早嘗試。但是三次、四次方程的一般解法(即給出求根公式),直到15世紀末也還沒有被發現。義大利數學家帕喬利在1494年出版的著作中還說:“x +mx=n,x +n=mx(m,n為正數)現在之不可解,正像化圓為方問題一樣。”但到16世紀上半葉,三次方程的一般解法就由義大利數學家費羅、塔爾塔利亞和卡爾達諾等得到,三次方程的求根公式最早出現在卡爾達諾的《大術》(1545)之中。四次方程的求根公式由卡爾達諾的學生費拉里首先得到,也記載於卡爾達諾的《大術》中。
在16世紀末到17世紀上半葉,數學家們還探討如何判定方程的正根、負根和復根的個數。卡爾達諾曾指出一個實係數方程的復根是成對出現的,牛頓在他的《廣義算術》中證明了這一事實。笛卡兒在他的《幾何學》中給出了正負號法則(通稱笛卡兒法則),即多項式方程f(x)=0的正根的最多數目等於係數變號的次數,而負根的最多數目等於兩個正號和兩個負號連續出現的次數。但笛卡兒本人沒有給出證明,這個法則是18世紀的幾個數學家證明的。牛頓在《廣義算術》中給出確定正負根數目上限的另一法則,並由此推出至少能有多少個複數根。
研究代數方程的根與係數之間的關係,也是這一時期代數學的重要課題。卡爾達諾發現方程所有根的和等於x的係數取負值,每兩個根的乘積之和等於x的係數,等等。韋達和牛頓也都在他們的著作中分別敘述了方程的根與係數之間的關係,現在稱這個結果為韋達定理。這些工作在18世紀發展為關於根的對稱函式的研究。
另一個重要課題是今天所謂的因子定理。笛卡兒在他的《幾何學》中指出,f(x)能為(x-a)整除,若且唯若a是f(x)=0的一個根。由此及其他結果,笛卡兒建立了求多項式方程有理根的現代方法。他通過簡單的代換,把方程的首項係數化為1,並使所有係數都變為整數,這時他判斷,原方程的各有理根必定是新方程常數項的整數因子。牛頓還發現了方程的根與其判別式之間的關係,他在《廣義算術》中還給出了確定方程根的上界的一些定理。此外,數學歸納法也在18世紀末開始明確地用於代數學中。
18世紀以後,數學家們的注意力開始轉向尋求五次以上方程的根式解。經過兩個多世紀的努力,在歐拉、旺德蒙德、拉格朗日、魯菲尼等人工作的基礎上,在19世紀上半葉,阿貝爾和伽羅瓦幾乎同時證明了五次以上的方程不能用公式求解。他們的工作開創了用群論的方法來研究代數方程的解的理論,為抽象代數學的建立開闢了道路(見置換群和伽羅瓦理論)。
代數方程理論的另一個問題是“一個方程能有多少個根”。中世紀阿拉伯和印度的數學家們都已認識到二次方程有兩個根。到了16世紀,義大利數學家卡爾達諾引入了複數根,並認識到一個三次方程有3個根,一個四次方程有4個根,等等。荷蘭數學家吉拉爾在1629年曾推測並斷言:任意一個n次方程,如果把復根算在內並且k重根算作k個根的話,那么它就有n個根。這就是代數基本定理。這個定理在18世紀被許多著名的數學家認識到並試圖證明之,直到1799年高斯才給出第一個實質性的證明。
對代數方程理論的研究,使數學家們引進了在近世代數中具有頭等重要意義的新概念,這些新概念很快被發展成為有廣泛套用的代數理論。
倒數方程
倒數方程亦稱反商方程。一種特殊方程。即根的倒數亦為其根的整式一元方程。如果一元n次方程f(x)=0的根和f(1/x)=0的根完全相同,則稱f(x)=0是一元n次倒數方程。它有下面兩種形式:
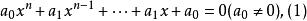 互反方程
互反方程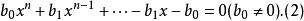 互反方程
互反方程方程(1)稱為第一類型倒數方程,亦稱互反方程;方程(2)稱為第二類型倒數方程。它的特點是首項係數和常數項,x的n-1次項係數和一次項係數,…,x的n-k次項係數和x的k次項係數,或是都相等,或是都相差一個負號。當n為偶數時,設n=2m,倒數方程可寫為:
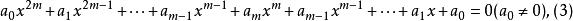 互反方程
互反方程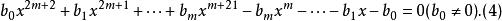 互反方程
互反方程方程(3)稱為第一類型偶次倒數方程,方程(4)稱為第二類型偶次倒數方程。應該注意到方程(4)正中間的一項係數b為零。當n為奇數時,設n=2m+1,倒數方程可寫為:
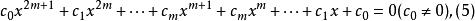 互反方程
互反方程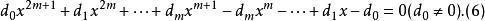 互反方程
互反方程方程(5)稱為第一類型奇次倒數方程,方程(6)稱為第二類型奇次倒數方程。第二類偶次倒數方程(4)有根±1,求出根±1後可以化為一個形如方程(3)的2m次方程;第一類奇次倒數方程(5)有根-1,求出根-1後也可以化為一個形如方程(3)的2m次方程;第二類奇次倒數方程(6)有根1,求出根1後仍可以化為一個形如方程(3)的2m次方程。因此,方程(4),(5),(6)分別求出根±1,-1或1以後,所得的降次方程都是第一類偶次倒數方程,所以,第一類偶次倒數方程又稱為標準型倒數方程。
