簡介
 交換子
交換子 交換子
交換子 交換子
交換子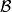 交換子
交換子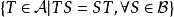 交換子
交換子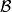 交換子
交換子 交換子
交換子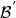 交換子
交換子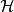 交換子
交換子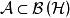 交換子
交換子 交換子
交換子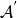 交換子
交換子設 是代數 的子集,稱 中與 內的所有元素都交換的元素構成的集合,即 ,為 在 中的交換子,記為 。設 是希爾伯特空間,如果 是自伴子代數,則 的交換子 也是自伴子代數,並且在強運算元拓撲下閉。
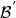 交換子
交換子 交換子
交換子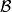 交換子
交換子 交換子
交換子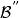 交換子
交換子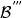 交換子
交換子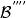 交換子
交換子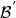 交換子
交換子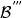 交換子
交換子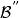 交換子
交換子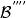 交換子
交換子稱 在中的交換子為在中的二次交換子(double commutant),記為。類似地,可以定義更高次的交換子,,...,此時,==...,==...。
交換子群
在抽象代數中,一個群的 換位子群或 導群,是指由這個群的所有交換子所生成的子群,記作[ G, G]、 G′或 G(1) 。每個群都對應著一個確定的交換子群。在一個群 G的所有正規子群中,交換子群 G′是使得 G對它的商群為交換群的最小子群。
在某種意義上,交換子群提供了群 G的可交換程度。因為從交換子的定義:[x,y]= xyx y ,如果x與y交換,那么[x,y]=e。一個群內可交換的元素越多,交換子就越少,交換子群也就越小。可交換群的交換子群為平凡群{e}。