簡介
被加數是求和法中的一項,類似於減法中的被減數,在加法中,被加數和加數的性質是一樣的,只不過為了和減法的被減數搭配起來一起學習而提出來的概念。
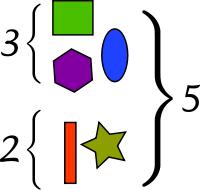
加法是基本的四則運算之一,它是指將兩個或者兩個以上的數、量合起來,變成一個數、量的計算。表達加法的符號為加號“+”。進行加法時以加號將各項連線起來。加法(通常用加號“+”表示)是算術的四個基本操作之一,其餘的是減法,乘法和除法。 例如,在下面的圖片中,共有三個蘋果和兩個蘋果的組合,總計五個蘋果。 該觀察結果等同於數學表達式“3 + 2 = 5”,即“3加2等於5”,3就可以看成被加數,2看成加數,5就是和。
 被加數
被加數解讀
加法已經被用於建立了無數的物理過程。 即使添加自然數的簡單情況,也有許多可能的解釋和更多的視覺表現。
組合
可能最基本的加法解釋在於組合:
當兩個或多個不相交的集合被組合成單個集合時,單個集合中的對象數量是原始集合中對象數量的總和。
這種解釋很容易可視化。 它也適用於高等數學;對於它激發的嚴格定義,請參見下面的自然數字。
一個可能的解決方案是考慮可以容易地分割的對象的集合,例如餡餅。桿不僅可以組成棒的集合,還可以將桿連線在一起,這又說明了加法的另一個概念:不添加棒,而是添加桿的長度。
 被加數
被加數延長一段長度
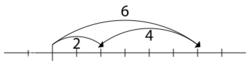
對加法的第二個解釋來自於將初始長度延長給定長度:
當原始長度延長給定量時,最終長度是原始長度和延伸長度之和,那么在這裡原始長度就可以看成被加數,延伸長度就是加數,最終長度就是和。
 被加數
被加數性質
一般來說,在一個集合F上定義一個二元關係“+”,滿足:
Ⅰ交換律:對任意的 a, b∈ F, a+ b= b+ a∈ F;
Ⅱ結合律:對任意的 a, b,c∈ F, a+ ( b+ c) = ( a+ b) + c;
Ⅲ單位元:存在一個元素 0 ∈ F,滿足對任意的 a ∈ F, a+ 0 = 0 + a= a;
Ⅳ 逆元:對任意的 a∈ F,存在一個元素 - a∈ F,滿足 a+ (- a) = 0。
“+”稱作定義在集合F上的加法。
“+”是加號,加號前面和後面的數是加數,“=”是等於號,等於號後面的數是和。
100(加數) +(加號) 300(加數) =(等於號) 400(和)
加法本質
是完全一致的事物也就是同類事物的重複或累計,是數字運算的開始,不同類比如一個蘋果+一個橘子其結果只能等於二個水果就存在分類與歸類的關係。減法是加法的逆運算;乘法是加法的特殊形式;除法是乘法的逆運算;乘方是乘法的簡便形式;開方是乘方的逆運算;對數是在乘方的各項中尋找規律;由對數而發展出導數;然後是微分和積分。數字運算的發展,是更特殊的情況,更高度重複下的規律。
