定義
B樹1970年，R.Bayer和E.mccreight提出了一種適用於外查找的樹，它是一種平衡的多叉樹，稱為B樹（或B-樹、B_樹）。
一棵m階B樹(balanced tree of order m)是一棵平衡的m路搜尋樹。它或者是空樹，或者是滿足下列性質的樹：
1、根結點至少有兩個子女；
2、每個非根節點所包含的關鍵字個數 j 滿足：┌m/2┐ - 1 <= j <= m - 1；
3、除根結點以外的所有結點（不包括葉子結點）的度數正好是關鍵字總數加1，故內部子樹個數 k 滿足：┌m/2┐ <= k <= m ；
4、所有的葉子結點都位於同一層。
在B-樹中，每個結點中關鍵字從小到大排列，並且當該結點的孩子是非葉子結點時，該k-1個關鍵字正好是k個孩子包含的關鍵字的值域的分劃。
因為葉子結點不包含關鍵字，所以可以把葉子結點看成在樹里實際上並不存在外部結點，指向這些外部結點的指針為空，葉子結點的數目正好等於樹中所包含的關鍵字總個數加1。
B-樹中的一個包含n個關鍵字，n+1個指針的結點的一般形式為： （n,P0,K1,P1,K2,P2,…,Kn,Pn）
其中，Ki為關鍵字，K1<…
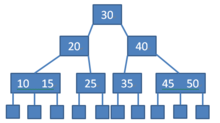
示例
當在葉子結點處於第L+1層的B樹中插入關鍵字時，被插入的關鍵字總是進入第L層的結點。
若在一個包含j
插入算法演示：插入之前如圖1：
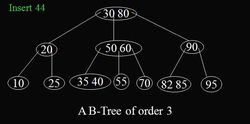插入之前的B樹插入之後如圖2：
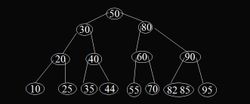插入之後的B樹4. B-樹的刪除:
當從B-樹中刪除一個關鍵字Ki時，總的分為以下兩種情況：
如果該關鍵字所在的結點不是最下層的非葉子結點，則先需要把此關鍵字與它在B-樹中後繼對換位置，即以指針Pi所指子樹中的最小關鍵字Y代替Ki，然後在相應的結點中刪除Y。
如果該關鍵字所在的結點正好是最下層的非葉子結點，這種情況下，會有以下兩種可能：
① 若該關鍵字Ki所在結點中的關鍵字個數不小於┌m/2┐，則可以直接從該結點中刪除該關鍵字和相應指針即可。
② 若該關鍵字Ki所在結點中的關鍵字個數小於┌m/2┐，則直接從結點中刪除關鍵字會導致此結點中所含關鍵字個數小於┌m/2┐-1 。這種情況下，需考察該結點在B樹中的左或右兄弟結點，從兄弟結點中移若干個關鍵字到該結點中來（這也涉及它們的雙親結點中的一個關鍵字要作相應變化），使兩個結點中所含關鍵字個數基本相同；但如果其兄弟結點的關鍵字個數也很少，剛好等於┌m/2┐-1 ，這種移動則不能進行，這種情形下，需要把刪除了關鍵字Ki的結點、它的兄弟結點及它們雙親結點中的一個關鍵字合併為一個結點。
