二倍角公式

二倍角公式，是繼三角函式的誘導公式和兩角和與差的正弦、餘弦、正切公式之後的又一重要公式。它為研究三角恆等式及三角函式等問題提供了又一必備的工具。數學公式，包含了正弦二倍角公式、餘弦二倍角公式、正切二倍角公式等。

基本信息

• 中文名稱：二倍角公式

• 類型：公式
• 拼音：èr bèi jiǎo gōng shì
• 推導公式：sin2α=2sinαcosα

正弦二倍角

sin2α = 2cosαsinα

推導：

sin2A = sin(A+A) = sinAcosA + cosAsinA = 2sinAcosA

餘弦二倍角

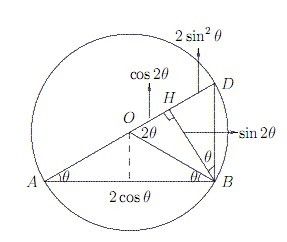餘弦二倍角

餘弦二倍角公式有三組表示形式，三組形式等價：
1、cos2α=2cos^2α-1
2、cos2α=1−2sin^2α
3、cos2α=cos^2α−sin^2α
推導：
cos2A=cos(A+A)=cosAcosA-sinAsinA=cos^2A-sin^2A=2cos^2A-1=1-2sin^2A

正切二倍角

tan2α=2tanα/[1-(tanα)^2]
tan(1/2*α)=(sinα)/(1+cosα)=(1-cosα)/sinα

推導：

tan(2a)=tan(a+a)=（tan(a)+tan(a)）/（1-tan(a)*tan(a)）=2tanα/[1-(tanα)^2]

降冪(半角）

tan2A=2tanA/[1-(tanA)^2]
cos2a=(cosa)^2-(sina)^2=2(cosa)^2-1=1-2(sina)^2
（上面這個餘弦的很重要）
sin2A=2sinA*cosA
半角的只需記住這個：
tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA)
用二倍角中的餘弦可推出降冪公式
(sinA)^2=(1-cos2A)/2
(cosA)^2=(1+cos2A)/2
用以上降冪公式可推出以下常用的化簡公式
1-cosA=sin^(A/2)*2
1-sinA=cos^(A/2)*2