不定積分的運算法則，包含如下兩個性質（注意性質適用條件）：
1、設函式f(x)的原函式存在（即f(x)可積，下同），k是常數，則：
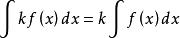不定積分的運算法則（1） （k≠0）
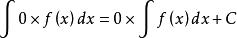不定積分的運算法則（2） （k=0）
2、設f(x)，g(x)兩個函式存在原函式，則：
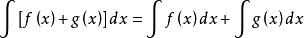不定積分的運算法則3、常見積分幾種運算法
換元積分法：
不定積分的運算法則 不定積分的運算法則①設f(u)具有原函式F(u) ，如果u是中間變數：u= (x),且 (x)可微，那么，根據複合函式微分法，有
不定積分的運算法則 不定積分的運算法則 不定積分的運算法則dF=[ (x)]=f[ (x)] '(x)dx，從而根據不定積分的定義就得：
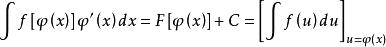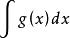不定積分的運算法則
不定積分的運算法則
不定積分的運算法則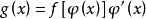
不定積分的運算法則若要求
，若可化為的形式，那么：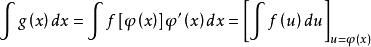
不定積分的運算法則這種方法稱為第一類換元法。
②利用第二類換元法化簡不定積分的關鍵仍然是選擇適當的變換公式 x = φ(t)。此方法主要是求無理函式(帶有根號的函式)的不定積分。由於含有根式的積分比較困難，因此我們設法作代換消去根式，使之變成容易計算的積分。 下面簡單介紹第二類換元法中常用的方法：
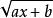不定積分的運算法則 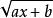不定積分的運算法則（1）根式代換：被積函式中帶有根式 ，可直接令 t =
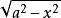不定積分的運算法則
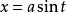不定積分的運算法則
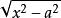不定積分的運算法則
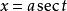不定積分的運算法則（2）三角代換：利用三角函式代換，變根式積分為有理函式積分，有三種類型： 被積函式含根式 ，令 ；被積函式含根式 ，令 。
註：記住三角形示意圖可為變數還原提供方便。
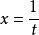不定積分的運算法則（3）倒代換（即令 ）：設m,n 分別為被積函式的分子、分母關於x 的最高次數，當 n-m>1時，用倒代換可望成功
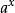不定積分的運算法則（4）指數代換：適用於被積函式由指數 所構成的代數式；
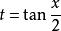不定積分的運算法則（5）萬能代換（半角代換）：被積函式是三角函式有理式，可令 ，則：
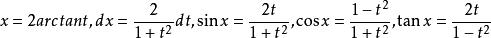不定積分的運算法則分部積分法：
設函式u=u(x)及v=v(x)具有連續導數，則其乘積的導數為：
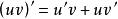不定積分的運算法則，移項得：
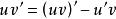不定積分的運算法則對兩邊求不定積分，得：
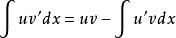不定積分的運算法則
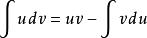不定積分的運算法則也可寫為：
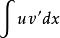不定積分的運算法則
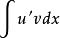不定積分的運算法則如果求 有困難，而求 比較容易時，分部積分公式就可以發揮作用了。
