描述
定義
把向量外積定義為：
符號表示： a× b
大小：| a|·| b|·sin< a, b>.
方向：右手定則：若坐標系是滿足右手定則的，設 z= x× y,| z|=| x|| y|*sin< x, y>；則 x, y, z構成右手系，伸開右手手掌，四個手指從x軸正方向方向轉到y軸正方面，則大拇指方向即為z正軸方向。
外積的坐標表示：
(x,y,z×(x,y,z)=(yz-yz,zx-zx,xy-xy
分配律
a× ( b+c) = a × b + a × c
分配律的幾何證明方法很繁瑣，大意是用作圖的方法驗證。有興趣的話請自己參閱參考文獻中的證明。
下面給出代數方法。我們假定已經知道了：
1）外積的反對稱性：
a× b= - b× a.
這由外積的定義是顯然的。
2）內積（即數積、點積）的分配律：
a·（ b+ c) = a· b+ a· c,
（ a+ b）· c= a· c+ b· c.
這由內積的定義 a· b= | a|·| b|·cos< a, b>；，用投影的方法不難得到證明。
3）混合積的性質：
定義（ a× b）· c為矢量 a, b, c的混合積，容易證明：
外積i) ( a× b）· c的絕對值正是以 a, b, c為三條鄰棱的平行六面體的體積，其正負號由 a, b, c的定向決定（右手係為正，左手係為負）。
簡單證明：體積V=底面積S×高h
=| a× b|×| h|
=| a× b|×| c|×( c· h)/(| c|| h|)
=| a× b|×( c· h)/| h|
而| h|=| a× b|
所以 V= c· h=c·( a× b）
從而就推出：
ii) ( a× b）· c= a·（ b× c)
所以我們可以記 a, b, c的混合積為（ a, b, c).
由i）還可以推出：
iii) ( a, b, c) = ( b, c, a) = ( c, a, b)
我們還有下面的一條顯然的結論：
iv) 若一個矢量 a同時垂直於三個不共面矢 a1, a2, a3，則 a必為零矢量。
分配律證明
下面我們就用上面的1）2）3）來證明外積的分配律。
設 r為空間任意矢量，在 r·( a×( b+ c))里，交替兩次利用3）的ii）、iii）和數積分配律2），就有
r·( a×( b + c))
= ( r× a)·( b+ c)
= ( r× a)· b+ ( r× a)· c
= r·( a× b) + r·( a× c)
= r·( a× b+ a× c)
移項，再利用數積分配律，得
r·（ a×（ b+ c) - ( a× b+ a× c)) = 0
這說明矢量 a×（ b+ c) - ( a× b+ a× c)垂直於任意一個矢量。按3）的iv），這個矢量必為零矢量，即
a×（ b+ c) - ( a× b+ a× c) = 0
所以有
a×（ b+ c) = a× b+ a× c.
證畢。
二重向量外積
向量二重外積公式： a × ( b× c )= b( a · c) − c( a · b)
抽象定義
外積
外積
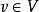外積
外積
外積給定向量和余向量，張量積給出映射，在同構之下。
外積具體的說，給定，
外積
外積
外積這裡的是在 w上的求值，它生成一個標量，接著乘 v。
外積
外積可作為替代，它是與的複合。
外積
外積如果，則還可以配對，這是內積。
