可導性與連續性
如果 f是在 x處可導的函式,則 f一定在 x處連續,特別地,任何可導函式一定在其定義域內每一點都連續。反過來並不一定。事實上,存在一個在其定義域上處處連續函式,但處處不可導。
魏爾斯特拉斯函式
魏爾斯特拉斯函式 是由魏爾斯特拉斯構造出的一個函式,其在R上處處連續,但處處不可導。
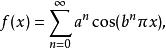 可導函式
可導函式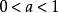 可導函式
可導函式 可導函式
可導函式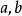 可導函式
可導函式其中 , 是正奇數,且 滿足
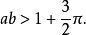 可導函式
可導函式可導函式類
 可導函式
可導函式 可導函式
可導函式 可導函式
可導函式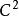 可導函式
可導函式 可導函式
可導函式 可導函式
可導函式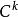 可導函式
可導函式 可導函式
可導函式 可導函式
可導函式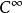 可導函式
可導函式稱 是 連續的,如果其導函式存在且是連續的。稱 是 連續的,如果其導數是 的。一般地,稱 是 連續的,如果其1階,直到k階導數存在且是連續的。若 任意階導數存在,則稱 是光滑的,或 的。
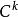 可導函式
可導函式全體 函數類構成Banach空間。
高維可導性
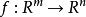 可導函式
可導函式 可導函式
可導函式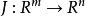 可導函式
可導函式稱 在 處可導,如果存在一線性映射 滿足
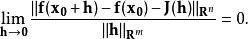 可導函式
可導函式 可導函式
可導函式 可導函式
可導函式如果 在定義域上任意點可導,則稱為可導函式。
注意:高維函式的偏導數存在,不一定可導。
例子
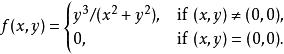 可導函式
可導函式在(0,0)處不可導,但是偏導數存在。
複函數的可導性
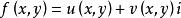 可導函式
可導函式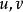 可導函式
可導函式在複分析中,稱函式是可導的,如果函式在定義域中每一點處是全純的。複函數可導等價於Cauchy–Riemann方程 。即,若可導當僅當滿足下列方程:
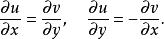 可導函式
可導函式或等價地寫成
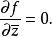 可導函式
可導函式流形上函式的可導性
 可導函式
可導函式 可導函式
可導函式流形上的函式稱為可導的,如果在任意的局部坐標系下,的局部表示是可導函式。
