sr[立體角的國際單位]

球面度(Sr=Steradian)是立體角的計量單位。面積為半徑平方(r)的球表面對球心的張角等於1球面度。因為球的表面積是4πr，所以，整個球面有4π球面度。一個發光強度等於1坎德拉的理想光源，每球面度能夠產生1流明光通量 。

定義

解釋1

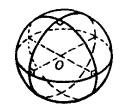圖1

球面度(spherical degree) 凡球均可分為八個相等的三直角球面三角形，把每個球面三角形分成90等分，稱每一等分為一 球面 度，因而任一球都有720球面度 。

解釋2

球面度(steradian)

sr；球面度

立體角的SI單位。是一立體角，其頂點位於球心，而它在球面上所截取的面積等於以球半徑為邊長的正方形面積 ：

sr[立體角的國際單位]

解釋3

球面度(立體角)：“立體角”是從球體的中心看過去的角度，它涵蓋球體表面上給定的區域。如果沒有量綱，則立體角是以球面度(sr)標籤給出的。1個球面度是指所切割下來的球體表面的面積等於與該球體半徑等邊長的正方形所具有的面積時所對應的立體角度，所切割下的表面的頂點處在球體的中心上。立體角的數值等於面積除以球體半徑的平方 。

解釋4

球面度：以球面積度量其所對應的立體角時的度量單位，該立體角的頂點位於球心處。

球面度的單位：若球面上有一圓形表面積或其他形狀的表面積，剛好與該球半徑r的平方相等時，則該面積對應之球心所張的立體角為1球面度sr(Steradian)。

sr[立體角的國際單位]

sr[立體角的國際單位]

由於球面積為，故此全部立體角為球面度 。

解釋5

sr[立體角的國際單位]

球面度(Sr=Steradian)是立體角的計量單位。面積為半徑平方(r)的球表面對球心的張角等於1球面度。因為球的表面積是，所以，整個球面有4π球面度。一個發光強度等於1坎德拉的理想光源，每球面度能夠產生1流明光通量 。

基本介紹

立體角單位—球面度(sr) 球面度是一立體角，其頂點位於球心，而它在球面上所截取的面積等於以球半徑為邊長的正方形面積，如圖1所示 。

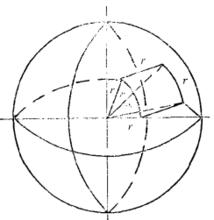圖1

立體角的單位球面度由下式求得

sr[立體角的國際單位]

sr[立體角的國際單位]

式中： ——中心位於立體角頂點的立體角割切球面的正方形面積；

sr[立體角的國際單位]

——球面的半徑。

sr[立體角的國際單位]

sr[立體角的國際單位]

一個完整的球面等於 球面度。球面度是無量綱的幾何量量度單位，直接測量立體角球面度的設備是沒有的，一般通過圓錐頂的平面角 並用下式

sr[立體角的國際單位]

進行球面度的測量。

sr[立體角的國際單位]

sr[立體角的國際單位]

sr[立體角的國際單位]

sr[立體角的國際單位]

sr[立體角的國際單位]

如：1球面度的立體角對應著圓錐邊間的 平面角； 球面度的立體角對應著 平面角(球的四分之一)； 球面度對應著 平面角(球的一半) 。