簡介
按照一定的規則,由排成正方形的一組(n個)數(稱為元素)之乘積形成的代數和,稱為n階行列式。
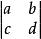 n階行列式
n階行列式例如,四個數a、b、c、d所排成二階行式記為 ,它的展開式為ad-bc。
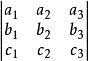 n階行列式
n階行列式九個數a,a,a;b,b,b;c,c,c排成的三階行列式記為 ,它的展開式為abc+abc+abc-abc-abc-abc. 行列式起源於線性方程組的求解,在數學各分支有廣泛的套用。在代數上,行列式可用來簡化某些表達式,例如表示含較少未知數的線性方程組的解等。
在1683年,日本的關孝和最早提出了行列式的概念及它的展開法。萊布尼茲在1693年(生前未發表)的一封信中,也宣布了他關於行列式的發現。
定義
定義1 n階行列式
 n階行列式
n階行列式等於所有取自不同行不同列的n個元素的乘積
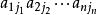 n階行列式
n階行列式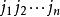 n階行列式
n階行列式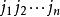 n階行列式
n階行列式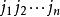 n階行列式
n階行列式的代數和,這裡 是1,2,...,n的一個排列,每一項都按下列規則帶有符號:當 是偶排列時帶有正號,當 是奇排列時帶有負號。這一定義可寫成
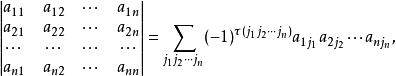 n階行列式
n階行列式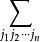 n階行列式
n階行列式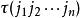 n階行列式
n階行列式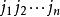 n階行列式
n階行列式這裡 表示對所有n級排列求和, 表示排列 的逆序數。
由定義1立即看出,n階行列式是由n! 項組成的。
n階行列式的性質
性質1 行列互換,行列式不變。
性質2 把行列式中某一行(列)的所有元素都乘以一個數K,等於用數K乘以行列式。
性質3 如果行列式的某行(列)的各元素是兩個元素之和,那么這個行列式等於兩個行列式的和。
性質4 如果行列式中有兩行(列)相同,那么行列式為零。(所謂兩行(列)相同就是說兩行(列)的對應元素都相等)
性質5 如果行列式中兩行(列)成比例,那么行列式為零。
性質6 把一行(列)的倍數加到另一行(列),行列式不變。
性質7 對換行列式中兩行(列)的位置,行列式反號。
n階行列式的計算
首先給出代數餘子式的定義。
定義2 在行列式
 n階行列式
n階行列式中划去元素a所在的第i行第j列,剩下的(n-1) 個元素按原來的排法構成一個n-1階的行列式M,稱M為元素a的餘子式,A=(-1) M稱為元素的代數餘子式。
定理 設
 n階行列式
n階行列式A表示元素a代數餘子式,則下列公式成立:
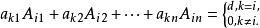 n階行列式
n階行列式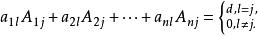 n階行列式
n階行列式范德蒙德行列式
行列式
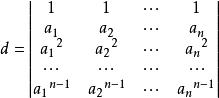 n階行列式
n階行列式稱為n級的范德蒙德(Vandermonde)行列式。可以證明:對任意的 n(n≥2),n階范德蒙德行列式等於a,a,...,a這n個數的所有可能的差a-a(1≤j<i≤n)的乘積。

