基本介紹
三角形行列式(triangular determinant)是一種特殊的行列式，數域P上形如
上三角行列式或
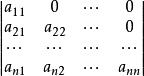上三角行列式的行列式分別稱為 上三角形行列式和 下三角形行列式，亦稱 上三角行列式和 下三角行列式，統稱 三角形行列 式。每個行列式都可以只運用行或者列的性質化為一個與其相等的上(下)三角形行列式。上(或下)三角形行列式都等於它們主對角線上元素的乘積。行列式
上三角行列式稱為 對角形行列式，亦稱 對角行列式。它既是一個上三角形行列式，又是一個下三角形行列式 。
行列式的七條性質
1. 行列式D與它的轉置行列式相等。
2. 互換行列式的兩行(列)，行列式的值改變符號。
由性質2可得出：如果行列式有兩行(列)的對應元素相同或成比例，則這個行列式為零。
3. n階行列式等於任意一行(列)的所有元素與其對應的代數餘子式的乘積之和。即
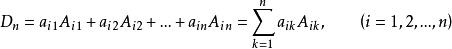上三角行列式或
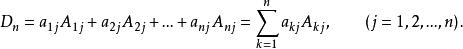上三角行列式性質3說明了行列式可按任一行或任一列展開。一般地，如果行列式的某一行或某一列中零元素較多；則按該行或該列展開來計算行列式會簡便一些。
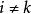上三角行列式4.n階行列式中任意一行(列)的所有元素與另一行(列)的相應元素的代數餘子式的乘積之和等於零。即當時有
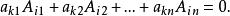上三角行列式由性質3和性質4，可得到如下結論：
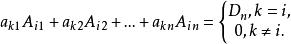上三角行列式
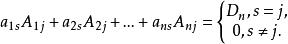上三角行列式5.行列式某一行(列)的公因子可以提出來。即用一個數乘行列式就等於用這個數乘行列式的某一行或某一列。
6.如果行列式中某- 一行(列)的元素可寫成兩數之和，則這個行列式等於兩個行列式的和，而且這兩個行列式除了這一行(列)以外，其餘的元素與原行列式的對應元素相同。
7. 將行列式的某一行(列)的各元素都乘以同一個常數後，再加到另一行(列)的對應元素上，其值不變 。
化行列式為上三角行列式
利用以下三條性質，可以把所給n階行列式化為上三角行列式，從而算出這個行列式的值。
(1) 互換行列式中某兩行(或某列)位置，行列式前乘(-1)；
(2) 行列式中某行(或某列)有公因子，這個公因子可以提到行列式外面去；
(3) 把行列式的某一行(或某一列)的任意倍加到另一行(或另一列)上去，行列式的值不變 。
例1計算四階行列式
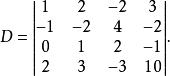上三角行列式解： 利用上述行列式的第三條性質，把第一行的1倍加到第二行上去，再把第一行的(-2)倍加到第四行上去
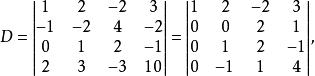上三角行列式(再互換第二行和第三行的位置)：
上三角行列式(將第二行的1倍加到第四行上去)：
上三角行列式(第四行提出公因子3後與第三行互換位置)：
上三角行列式(將第三行的-2倍加到第四行上去)：
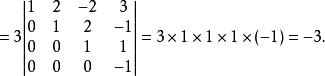上三角行列式