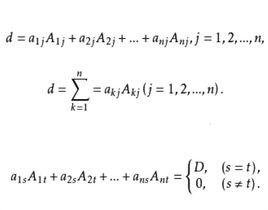基本介紹
設a，a，…，a(1≤j≤n)為n階行列式D=|a|的任意一列中的元素，而A，A，…，A分別為它們在D中的代數餘子式，則D=aA+aA+…+aA稱為行列式D的依列展開。
例如，在一個三階行列式D中，划去元素a(i=1, 2,3; j=1, 2,3)所在的第i行和第j列的所有元素，剩下的元素按照它原有的位置得到的一個二階行列式稱為元素a的餘子式，記作M。而將(-1)M稱為元素a的 代數餘子式，記作A，即A=(-1)M。例如
行列式依列展開行列式可按行或列展開，於是每個行列式可以表成它的某一行(或某一列)的每個元素與它對應元素的代數餘子式乘積的和，即
D= aA+ aA+ aA (i= 1, 2，3) ， (1)
D= aA+ aA+ aA (j=1，2, 3)， (1')
我們把類似(1)式的展開稱為行列式的依行展開式，把(1')式稱為行列式的依列展開式 。
相關定理
定理1 (行列式按列展開規則) n階行列式d等於它的任意一列元素與它們對應的代數餘子式之積的和，即
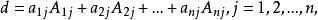行列式依列展開或
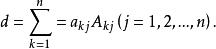行列式依列展開定理2如果行列式D的第s列各元素與第t列各元素的代數餘子式對應相乘後再相加，則當s≠t時，其和為零。因此有
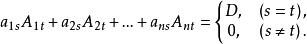行列式依列展開此定理也可以敘述為：n階行列式(n>1)的某列的元素與另一列的對應元素的代數餘子式乘積的和等於零 。
例題解析
【例1】計算：
行列式依列展開解：d中第5列零元素較多，應從這一列入手。
行列式依列展開按d中第6列展開得
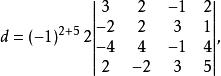行列式依列展開
行列式依列展開按第一列展開得
行列式依列展開說明在行列式計算中，我們經常利用行列式的展開把n階行列式轉化為n-1階行列式，通過降階逐步變為低階行列式後進行計算，但行列式按某一行或列展開時，只有在該行或列的元素有較多的零時，才能起到減少計算量的作用，因此往往先運用“化零”後進行“降階”，利用行列式性質降低行列式階數，然後計算行列式之值的方法稱為降階法，例1就是降階法的一例 。
