加邊行列式

加邊行列式(bordered determinant)是一種特殊行列式，有兩種解釋：一是指對一個n階行列式添加k行和k列(k為正整數)，而添加行列的交叉處補零所得到的(n+k)階行列式；二是指為了簡化行列式的運算，對n階行列式Dn增加一行、一列，就變成n+1階行列式△n+1，所得加邊行列式的值與原行列式的值相等。

基本介紹

（1）對一個n階行列式添加k行和k列(k為正整數)，且每行(列)各含有n個元素，而添加行列的交叉處補零所得到的(n+k)階行列式，叫做 加邊行列式。例如，行列式

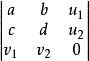加邊行列式

和

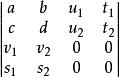加邊行列式

都是二階行列式

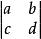加邊行列式

的加邊行列式 。

（2）行列式降一階，其項數急劇減少，我們總是喜歡用降階法處理問題，但是有時用升階法反而方便。對於n階行列式D增加一行，一列，就變成n+1階行列式△，由於增加的一行一列常常在邊上，稱△為n的 加邊行列式。構造出來的這個加邊行列式與原來的行列式值相等，而且這個加邊行列式容易計算 。

例題解析

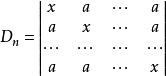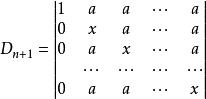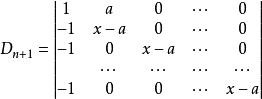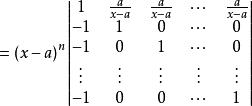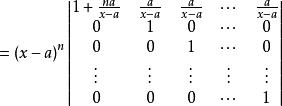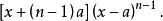加邊行列式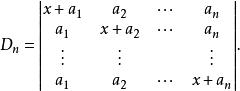

加邊行列式

加邊行列式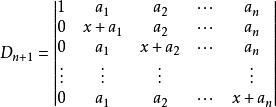

加邊行列式

加邊行列式

加邊行列式

加邊行列式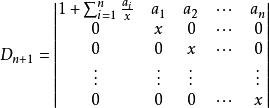

加邊行列式

加邊行列式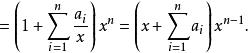

加邊行列式

加邊行列式

【例1】計算行列式： 解：D加邊成以下的n+1階行列式第一行乘以-1後分別加到其餘各行，再從第2，3，…，n+1列分別提取x-a，然後各列都加到第一列上，得當x=a時，Dn=0，以上結論也是對的。【例2】計算行列式： 解：將行列式升階 這是一個箭形行列式，當x不等於0時有 當x=0時，上述結果顯然也成立 。