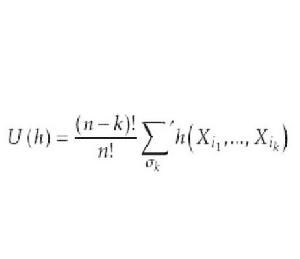基本介紹
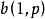 U統計量
U統計量 U統計量
U統計量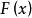 U統計量
U統計量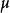 U統計量
U統計量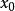 U統計量
U統計量估計問題有的是對特殊分布族的某個參數函式的估計,例如Bernoulli分布 的機率p的估計問題,也有一些是對廣泛的分布族 中分布F的某個特徵的估計問題,例如分布F的均值、方差或分布函式在某一點的函式值 的估計問題。對於分布的特徵均值 或分布函式在 的函式值也可寫成如下的形式:
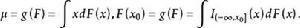 U統計量
U統計量在上述的表示中,如果將分布本身看作為一個“參數”,那么要估計的分布的特徵也是“參數”的函式。所以一般的可以考慮下列形式的特徵的估計問題:
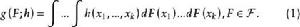 U統計量
U統計量 U統計量
U統計量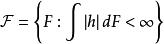 U統計量
U統計量這裡的分布族可以是較為廣泛的分布族 ,例如 。
式(1)中的h也稱為 參數函式g的核(kernel),k稱為核的階(order)。
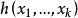 U統計量
U統計量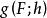 U統計量
U統計量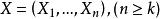 U統計量
U統計量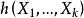 U統計量
U統計量對於以 為核的參數函式 , 一個基於樣本 的簡單的無偏估計是 ,但它只使用了樣本的前幾個觀測,為了利用所有的觀測,一個自然的做法是對稱化 。
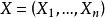 U統計量
U統計量定義 基於樣本 的統計量
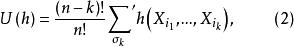 U統計量
U統計量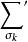 U統計量
U統計量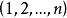 U統計量
U統計量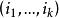 U統計量
U統計量稱為 U-統計量(U statistics),h也稱為統計量的 核。(2)中的 表示對 中取k個元素的排列 求和 。
相關性質
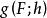 U統計量
U統計量(1)以h為核的U-統計量是h對應的參數函式 的無偏估計。
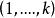 U統計量
U統計量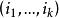 U統計量
U統計量(2)由於對 的任一個排列 成立
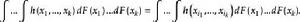 U統計量
U統計量所以不妨只考慮關於其變數為對稱的核h,即h滿足條件
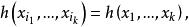 U統計量
U統計量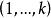 U統計量
U統計量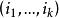 U統計量
U統計量對 的任一個排列 成立。
(3)對於對稱的k階核h,其U-統計量可寫為
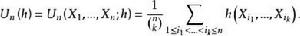 U統計量
U統計量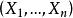 U統計量
U統計量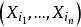 U統計量
U統計量(4)U-統計量關於 的任一排列 是不變的,所以它是只依賴於樣本順序統計量的函式 。
統計量
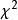 U統計量
U統計量 U統計量
U統計量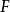 U統計量
U統計量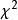 U統計量
U統計量 U統計量
U統計量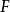 U統計量
U統計量統計量(statistic)是指樣本的已知函式,其作用是把樣本中有關總體的信息匯集起來,是數理統計學中一個重要的基本概念。常用統計量有樣本矩、次序統計量、U統計量和秩統計量等。其中U統計量是W.霍夫丁於1948年引進的。統計量的充分性和完全性是兩個重要概念,充分性是費希爾在1925年引進的,內曼和P.R.哈爾莫斯在1949年嚴格證明了一個判定統計量充分性的方法,叫做 因子分解定理。統計量的分布叫做 抽樣分布,它的研究是數理統計中的重要課題。對一維正態總體,有三個重要的抽樣分布,即 分布、 分布和 分布。其中 分布是F.赫爾梅特於1875年在研究正態總體的樣本方差時得到的; 分布是英國統計學家W.S.戈塞特(筆名“學生”)於1908年提出的; 分布是費希爾在20世紀20年代提出的 。