定義
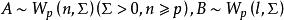 Wilks統計量
Wilks統計量設,且A與B相互獨立,則我們稱隨機變數
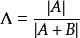 Wilks統計量
Wilks統計量 Wilks統計量
Wilks統計量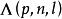 Wilks統計量
Wilks統計量為Wilks變數,它服從的分布記為。
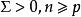 Wilks統計量
Wilks統計量 Wilks統計量
Wilks統計量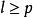 Wilks統計量
Wilks統計量 Wilks統計量
Wilks統計量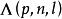 Wilks統計量
Wilks統計量注 在定義中要求以保證A機率為1正定,而對沒有的要求,當p=1時它正是一元統計中的分布,它最早是Wilks提出的。當p≥3時的精確分布的密度表達式是很複雜的 。
相關定理及結論
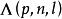 Wilks統計量
Wilks統計量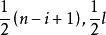 Wilks統計量
Wilks統計量 Wilks統計量
Wilks統計量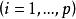 Wilks統計量
Wilks統計量定理1的分布正是由p個相互獨立且依次服從參數為的分布的隨機變數的乘積所服從的分布。
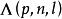 Wilks統計量
Wilks統計量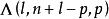 Wilks統計量
Wilks統計量定理2和服從相同的分布。
 Wilks統計量
Wilks統計量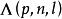 Wilks統計量
Wilks統計量 Wilks統計量
Wilks統計量 Wilks統計量
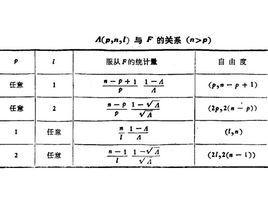
Wilks統計量利用定理1和2可以求出當p=1,2或=1,2時的確切分布。關於p=1,2或者= 1,2時的分布與F分布的關係由表1式給出。
| p |  Wilks統計量 Wilks統計量 | 服從F的統計量 | 自由度 |
| 任意 | 1 | 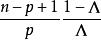 Wilks統計量 Wilks統計量 | 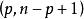 Wilks統計量 Wilks統計量 |
| 任意 | 2 | 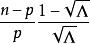 Wilks統計量 Wilks統計量 | 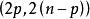 Wilks統計量 Wilks統計量 |
| 1 | 任意 | 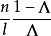 Wilks統計量 Wilks統計量 | 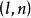 Wilks統計量 Wilks統計量 |
| 2 | 任意 | 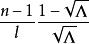 Wilks統計量 Wilks統計量 | 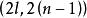 Wilks統計量 Wilks統計量 |
 Wilks統計量
Wilks統計量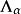 Wilks統計量
Wilks統計量正如F分布對於一元方差分析和回歸分析十分有用一樣,Λ統計量的分布對於多元方差分析和回歸分析也是十分重要的。關於Λ(p,n,l)對應於顯著水平的臨界值已經由前人造成表格,可參考相應書籍。有時為了方便,當n充分大的時候我們也可利用它的漸近分布求出臨界域,我們不加證明給出下面定理。
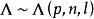 Wilks統計量
Wilks統計量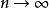 Wilks統計量
Wilks統計量定理3 設,則當行時
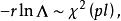 Wilks統計量
Wilks統計量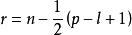 Wilks統計量
Wilks統計量其中。當n不太大時則有
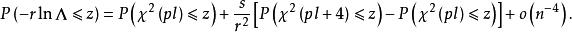 Wilks統計量
Wilks統計量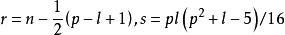 Wilks統計量
Wilks統計量其中,。
 Wilks統計量
Wilks統計量 Wilks統計量
Wilks統計量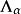 Wilks統計量
Wilks統計量此定理是Box(1949)給出的,讀者可根據顯著水平和n的大小從表中找到相應的臨界值。