JB統計量

JB統計量，即Jarque-Bera統計量，是用來檢驗一組樣本是否能夠認為來自正態總體的一種方法。

Jarque-Bera統計量是用來檢驗一組樣本是否能夠認為來自正態總體的一種方法。它依據OLS殘差，對大樣本進行檢驗（或稱為漸進檢驗）。
首先計算偏度係數S(對機率密度函式對稱性的度量)：

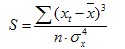
及峰度係數K(對機率密度函式的“胖瘦”的度量)：

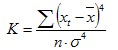
對於常態分配變數，偏度為零，峰度為3.
Jarque和Bera建立了如下檢驗統計量——JB統計量：

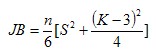
其中，n為樣本容量，S為偏度，K為峰度。
在常態分配的假設下，JB統計量漸進地服從自由度為2的卡方分布, JBasy~χ2(2)。
若變數服從常態分配，則S為零，K為3，因而JB統計量的值為零；如果變數不是正態變數，則JB統計量將為一個逐漸增大值。
如果JB統計量值較大，比如為11，則可以計算出卡方值大於11的機率為0.004，這個機率過小，因此不能認為樣本來自常態分配。反之，成立。