簡介
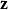Softmax函式
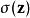Softmax函式
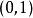Softmax函式在數學，尤其是機率論和相關領域中， Softmax函式，或稱 歸一化指數函式，是邏輯函式的一種推廣。它能將一個含任意實數的K維向量 “壓縮”到另一個K維實向量 中，使得每一個元素的範圍都在 之間，並且所有元素的和為1。
該函式的形式通常按下面的式子給出：
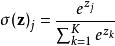Softmax函式其中， j = 1, …, K
Softmax函式實際上是有限項離散機率分布的梯度對數歸一化。因此，Softmax函式在包括多項邏輯回歸，多項線性判別分析，樸素貝葉斯分類器和人工神經網路等的多種基於機率的多分類問題方法中都有著廣泛套用。特別地，在多項邏輯回歸和線性判別分析中，函式的輸入是從K個不同的線性函式得到的結果，而樣本向量 x屬於第 j個分類的機率為：
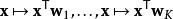Softmax函式
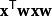Softmax函式這可以被視作K個線性函式 Softmax函式的複合（ ） 。
Softmax函式有關的例子
輸入向量[1,2,3,4,1,2,3]對應的Softmax函式的值為[0.024,0.064,0.175,0.475,0.024,0.064,0.175]。輸出向量中擁有最大權重的項對應著輸入向量中的最大值“4”。這也顯示了這個函式通常的意義：對向量進行歸一化，凸顯其中最大的值並抑制遠低於最大值的其他分量。
下面是使用Python進行函式計算的示例代碼：
Julia的範例：
Softmax 與 Sigmoid 的 異同
| Softmax | Sigmoid | |
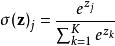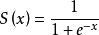| 公式 | Softmax函式 |  Softmax函式 |
| 本質 | 離散機率分布 | 非線性映射 |
| 任務 | 多分類 | 二分類 |
| 定義域 | 某個一維向量 | 單個數值 |
| 值域 | [0,1] | （0,1） |
| 結果之和 | 一定為1 | 為某個正數 |
Sigmoid就是極端情況(類別數為2)下的Softmax 。
