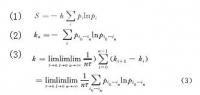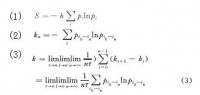柯爾莫哥洛夫熵
柯爾莫哥洛夫熵（以下簡稱K熵）是刻劃混沌系統的一個重要的量。在不同類型的動力學系統中，K熵的數值是不同的。K熵的數值可以用來區分規則運動、混沌運動和隨機運動。在隨機運動系統中，K熵是無界的；在規則運動系統中，K熵為零；在混沌運動系統中，K熵大於零，K熵越大，那么信息的損失速率越大，系統的混沌程度越大，或者說系統越複雜［3］。在資訊理論中，香農熵（Shannon熵，簡稱S熵）定義為
（1）
式中pi是系統處於狀態i的機率；h是與熵的單位有關的常數。根據香農的信息理論，S熵可用來刻劃對系統未知的程度，當S熵的數值大於零時，系統總存在我們無法認識的側面。
根據S熵的定義，可以引入K熵的定義如下：如果奇怪吸引子動力系統的軌道為x（t）={x1（t）,…,xd（t）},設d維空間被劃分成一系列尺寸為ld的盒子，系統的狀態可在時間τ的間隔內觀察，設pi0…in是x（0）在盒子i0中，x（τ）在盒子i1中，x（nτ）在盒子in中的聯合機率，根據香農公式有
（2）
它正比於以長度l確定系統在特殊軌道i*0,…,i*n所需要的信息。因此kn+1-kn是系統於已知單元i*0,…,i*n中和系統在預測單元i*n+1中的信息之差，這意味著kn+1-kn量度了系統從時間nτ到（n+1）τ的信息損失。K熵定義為信息的平均損失率為
極限l→0說明K熵與相空間的劃分無關。
圖片
