定義
數學上， 勒讓德函式指以下 勒讓德微分方程的解：
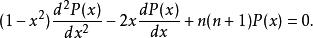Legendre多項式為求解方便一般也寫成如下施圖姆-劉維爾形式（Sturm-Liouville form）:
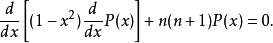Legendre多項式上述方程及其解函式因法國數學家阿德里安-馬里·勒讓德而得名。勒讓德方程是物理學和其他技術領域常常遇到的一類常微分方程。當試圖在球坐標中求解三維拉普拉斯方程（或相關的其他偏微分方程）時，問題便會歸結為勒讓德方程的求解。
勒讓德方程的解可寫成標準的冪級數形式。當方程滿足 | x| < 1 時，可得到有界解（即解級數收斂）。並且當 n為非負整數，即 n= 0, 1, 2,... 時，在 x= ± 1 點亦有有界解。這種情況下，隨 n值變化方程的解相應變化，構成一組由正交多項式組成的多項式序列，這組多項式稱為 勒讓德多項式（Legendre polynomials）。
勒讓德多項式P( x)是 n階多項式，可用羅德里格公式表示為：
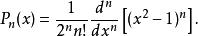Legendre多項式正交性
勒讓德多項式的一個重要性質是其在區間 −1 ≤ x≤ 1 關於L內積滿足正交性，即：
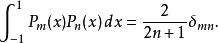Legendre多項式其中 δ為克羅內克δ記號，當 m= n時為1，否則為0。 事實上，推導勒讓德多項式的另一種方法便是關於前述內積空間對多項式{1, x, x, ...}進行格拉姆-施密特正交化。之所以具有此正交性是因為如前所述，勒讓德微分方程可化為標準的Sturm-Liouville問題：
Legendre多項式其中本徵值 λ 對應於原方程中的 n( n+1)。
其他性質
奇偶性
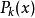Legendre多項式 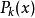Legendre多項式當階數 k為偶數時， 為偶函式；當階數 k為奇數時， 為奇函式，即：
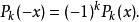Legendre多項式遞推關係
相鄰的三個勒讓德多項式具有三項遞推關係式：
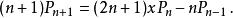Legendre多項式另外，考慮微分後還有以下遞推關係：
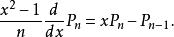Legendre多項式
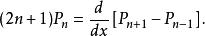Legendre多項式其中最後一個式子在計算勒讓德多項式的積分中較為有用。
移位多項式
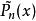Legendre多項式移位勒讓德多項式的正交區間定義在[0,1]上，即：
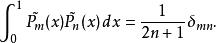Legendre多項式其顯式表達式為：
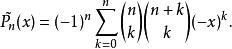Legendre多項式相應的羅德里格公式為：
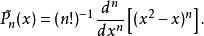Legendre多項式分數階多項式
分數階勒讓德多項式通過將分數階微分（定義參見分數微積分理論）和通過Γ函式定義的非整數階乘代入羅德里格公式中來定義。
極限關係
大Q勒讓德多項式→ 勒讓德多項式
令大q雅可比多項式中的c=0，即勒讓德多項式
令連續q勒讓德多項式q->1得勒讓德多項式
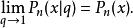Legendre多項式小q勒讓德多項式→ 勒讓德多項式
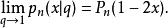Legendre多項式