一次函式
概念
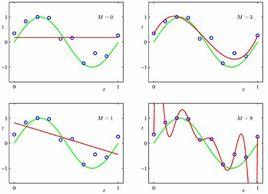
形如 y=kx+b (k為任意不為0的常數,b為任意常數)的函式叫做一次函式( linear function),也稱線性函式,其圖像在平面直角坐標系中可以用一條直線表示,當一次函式中的一個變數的值確定時,可以用一元一次方程確定另一個變數的值。
基本性質
1.y的變化值與對應的x的變化值成正比例,比值為k
即:y=kx+b(k≠0) (k不等於0,且k,b為常數)
2.當x=0時,b為函式在y軸上的交點,坐標為(0,b).
當y=0時,該函式圖象在x軸上的交點坐標為(-b/k,0)
3.k為一次函式y=kx+b的斜率,k=tanθ(角θ為一次函式圖象與x軸正方向夾角,θ≠90°)
形、取、象、交、減。
4.當b=0時(即 y=kx),一次函式圖象變為正比例函式,正比例函式是特殊的一次函式.
5.函式圖象性質:當k相同,且b不相等,圖像平行;
當k不同,且b相等,圖象相交於Y軸;
當k互為負倒數時,兩直線垂直;
6.平移時:上加下減在末尾,左加右減在中間 。
二次函式
介紹
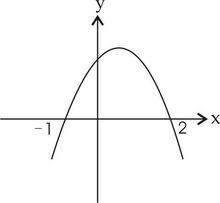 二次函式的圖像
二次函式的圖像一般地,形如 y=ax^2+bx+c的函式叫做二次函式( quadratic function)。二次函式是自變數的最高次數為二次的多項式函式。其圖像在平面直角坐標系中呈一條拋物線。
基本性質
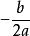 多項式函式
多項式函式1、二次函式的圖像是拋物線,但拋物線不一定是二次函式。開口向上或者向下的拋物線才是二次函式。拋物線是軸對稱圖形。對稱軸為直線x= 。對稱軸與拋物線唯一的交點為拋物線的頂點P。特別地,當b=0時,拋物線的 對稱軸是y軸(即直線x=0)。
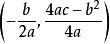 多項式函式
多項式函式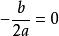 多項式函式
多項式函式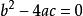 多項式函式
多項式函式2、拋物線有一個頂點P,坐標為P 。當 時,P在y軸上;當 時,P在x軸上。
3、二次項係數a決定拋物線的開口方向和大小。當a>0時,拋物線開口向上;當a<0時,拋物線開口向下。|a|越大,則拋物線的開口越小。|a|越小,則拋物線的開口越大。
4、一次項係數b和二次項係數a共同決定對稱軸的位置。當a與b同號時(即ab>0),對稱軸在y軸左側;當a與b異號時(即ab<0),對稱軸在y軸右側。(可巧記為:左同右異)
5、常數項c決定拋物線與y軸交點。拋物線與y軸交於(0, c)。
三次函式
 三次函式
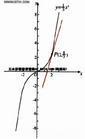
三次函式形如 y=ax^3+bx^2+cx+d (a≠0,b,c,d為常數)的函式叫做三次函式( cubics function)。三次函式的圖像是一條曲線——回歸式拋物線(不同於普通拋物線),具有比較特殊的性質。
基本性質
⒈三次函式y=f(x)在(-∞,+∞)上的極值點的個數;
⒉三次函式y=f(x)的圖象與x 軸交點個數;
⒊單調性問題;
⒋三次函式f(x)圖象的切線條數;
⒌融合三次函式和不等式,創設情境求參數的範圍。
特殊函式
除一次函式、二次函式、三次函式外,多項式函式的特殊形式還有四次函式、五次函式等 。