基本介紹
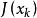L-M方法Gauss-Newton算法(1809)是一個古老的處理非線性最小二乘問題的方法，該方法在疊代過程中要求矩陣 列滿秩；而這一條件限制了它的套用。為克服這個困難，Levenberg(1944)提出了一個新的方法，但未受到重視。後來，Marquardt(1963) 又重新提出，並在理論上進行了探討，得到了Levenberg-Marquardt方法，簡稱L-M方法。再後來，Fletcher(1971) 對其實現策略進行了改進，得到了Levenberg- Marquardt-Fletcher方法。實際上，若將L-M方法與信賴域方法結合，效果可能更好 。
L-M方法通過求解下述最佳化模型來獲取搜尋方向：
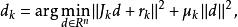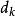L-M方法
L-M方法其中，μ> 0，由最優性條件知滿足
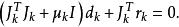L-M方法即
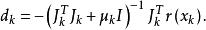L-M方法實際上，利用約束最佳化問題的最優性條件，L-M方法可以看作是Gause-Newton方法受信賴域方法的啟發產生的，因為d可視為下述約束最佳化問題的最優解
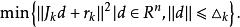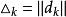L-M方法
L-M方法這裡，。
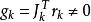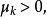L-M方法
L-M方法下面討論d的下降性質，若，則對任意,
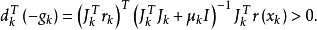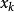L-M方法
L-M方法所以d是f(x) 在點的下降方向。引入線搜尋，我們便得到非線性最小二乘問題的L-M方法：
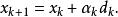L-M方法
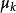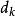L-M方法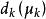 L-M方法
L-M方法由於d的取值與有關，所以從嚴格意義上講，應記為。
L-M方法與Gauss-Newton方法的區別在於前者的搜尋方向裡面引入了參數μ
相關結論
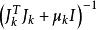L-M方法
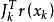L-M方法根據線性代數的知識，矩陣對向量的作用無非是改變後者的長度和方向，為此，對de(1k)，我們有下述結論。
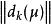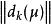L-M方法 L-M方法性質1關於μ> 0單調不增，且當μ→∞時，→0。
（文中性質的證明請見參考書）
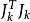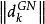L-M方法
L-M方法從幾何直觀來看，當矩陣接近奇異時，由Gauss-Newton算法得到的搜尋方向的模相當地大，而在L-M方法中，通過引入正參數μ就避免了這種情形出現。
下面看參數μ對搜尋方向角度的影響，
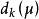L-M方法
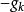L-M方法性質2與的夾角θ關於μ> 0單調不增。
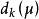L-M方法
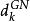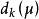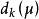L-M方法 L-M方法 L-M方法根據性質1和2，當μ=0時，就是Gauss-Newton方向。當μ> 0逐漸增大時，的長度逐漸縮短，方向則逐漸偏向最速下降方向，可以構想，當參數μ充分大時，的方向與目標函式的負梯度方向一致，不但如此，下面的結果表明，我們引入參數μ可以使得搜尋方向的求解更加趨於穩定，從而我們有理由相信L-M方法的數值效果應該比Gauss-Newon方法好一些。
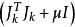L-M方法性質3的條件數關於μ單調不增。
基於以上討論，在具體的算法中，我們採用類似於調整信賴域半徑的策略來調整參數μ，這就得到Levenberg-Marquardt-Fletcher方法 。
套用範圍
Levenberg-Marquardt算法是最最佳化算法中的一種。最最佳化是尋找使得函式值最小的參數向量。它的套用領域非常廣泛，如：經濟學、管理最佳化、網路分析 、最優設計、機械或電子設計等等。
根據求導數的方法，可分為2大類。第一類，若f具有解析函式形式，知道x後求導數速度快。第二類，使用數值差分來求導數。根據使用模型不同，分為非約束最最佳化、約束最最佳化、最小二乘最最佳化。
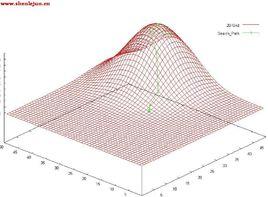
Levenberg-Marquardt算法是使用最廣泛的非線性最小二乘算法，中文為列文伯格-馬夸爾特法。它是利用梯度求最大（小）值的算法，形象的說，屬於“爬山”法的一種。它同時具有梯度法和牛頓法的優點。當λ很小時，步長等於牛頓法步長，當λ很大時，步長約等於梯度下降法的步長。圖1顯示了算法從起點，根據函式梯度信息，不斷爬升直到最高點（最大值）的疊代過程。共進行了12步。（備註：圖1中綠色線條為疊代過程）。
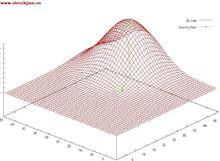圖1LM算法的實現並不算難，它的關鍵是用模型函式 f 對待估參數向量p在其領域內做線性近似，忽略掉二階以上的導數項，從而轉化為線性最小二乘問題，它具有收斂速度快等優點。LM算法屬於一種“信賴域法”，所謂的信賴域法，即是：在最最佳化算法中，都是要求一個函式的極小值，每一步疊代中，都要求目標函式值是下降的，而信賴域法，顧名思義，就是從初始點開始，先假設一個可以信賴的最大位移s，然後再以當前點為中心，以s為半徑的區域內，通過尋找目標函式的一個近似函式（二次的）的最優點，來求解得到真正的位移。在得到了位移之後，再計算目標函式值，如果其使目標函式值的下降滿足了一定條件，那么就說明這個位移是可靠的，則繼續按此規則疊代計算下去；如果其不能使目標函式值的下降滿足一定的條件，則應減小信賴域的範圍，再重新求解。
LM算法需要對每一個待估參數求偏導，所以，如果你的擬合函式 f 非常複雜，或者待估參數相當地多，那么可能不適合使用LM算法，而可以選擇Powell算法（Powell算法不需要求導）。
