定義
 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型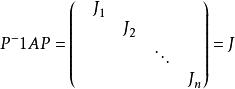 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型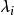 Jordan標準型
Jordan標準型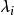 Jordan標準型
Jordan標準型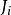 Jordan標準型
Jordan標準型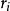 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型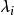 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型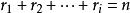 Jordan標準型
Jordan標準型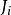 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型 Jordan標準型
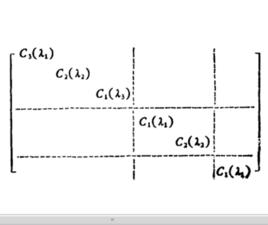
Jordan標準型對任一 階矩陣 ,必存在 階可逆陣 ,使 ,其中每一個對角塊都是Jordan塊: ,即對角線上同為 , 的上面都有一個1,其餘元素都是0, 是 階方陣。因此 中所有 都是矩陣 的特徵值, 。進一步,若不計各個Jordan塊 的排序, 是由 唯一確定的,也就是說, 的Jordan塊標準型,在不計Jordan塊次序的前提下,是唯一確定的。我們稱 稱為Jordan塊。
每個n階的複數矩陣A都與一個若爾當形矩陣相似,這個若爾當形矩陣除去其中若爾當塊的排列次序是被矩陣A唯一確定的,它成為矩陣A的若爾當標準型。
實例
Jordan陣
例如:
 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型, , , , 。
非Jordan陣
 Jordan標準型
Jordan標準型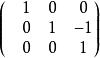 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型, , 。
相關定理
定理1
 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型設 是複數域上的n維線性空間上的線性變換.,在中必定存在一組基,使在這組基下的矩陣是若爾當形,並且這個若爾當形矩陣除去其中若爾當塊的排列次序是被唯一決定的。
定理2
 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型複數矩陣與對角矩陣相似的充分必要條件是,的初等因子全為一次的。
定理3
 Jordan標準型
Jordan標準型 Jordan標準型
Jordan標準型複數矩陣與對角矩陣相似的充分必要條件是,的不變因子都沒有重根。