定義
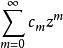 矩陣函式
矩陣函式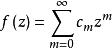 矩陣函式
矩陣函式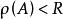 矩陣函式
矩陣函式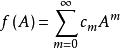 矩陣函式
矩陣函式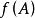 矩陣函式
矩陣函式設復變冪級數的收斂半徑是R,且在收斂域內,當矩陣A的譜半徑,定義,並稱為矩陣A的函式 。
常用的矩陣函式
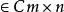 矩陣函式
矩陣函式(1)矩陣指數函式:對於任意A ,有:
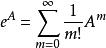 矩陣函式
矩陣函式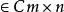 矩陣函式
矩陣函式(2)正弦函式,是一種矩陣三角函式:對於任意A,有:
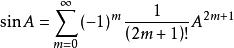 矩陣函式
矩陣函式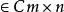 矩陣函式
矩陣函式(3)餘弦函式,是一種矩陣三角函式:對於任意A,有:
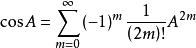 矩陣函式
矩陣函式定理
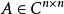 矩陣函式
矩陣函式1、定理1:假設,則有:
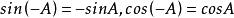 矩陣函式
矩陣函式(1);
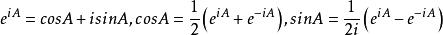 矩陣函式
矩陣函式(2)。
注意:因為矩陣的乘法不滿足交換律, 因此矩陣函式不一定滿足一般函式的所有性質。
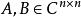 矩陣函式
矩陣函式2、定理2:設,且AB=BA,則有:
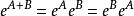 矩陣函式
矩陣函式(1);
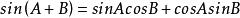 矩陣函式
矩陣函式(2);
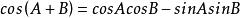 矩陣函式
矩陣函式(3)。
3、根據定理 2 ,很容易證得下面結論:
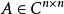 矩陣函式
矩陣函式推論 :設,則有:
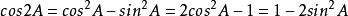 矩陣函式
矩陣函式(1);
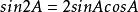 矩陣函式
矩陣函式(2);
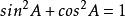 矩陣函式
矩陣函式(3)。
求解矩陣函式的方法
利用矩陣標準型
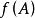 矩陣函式
矩陣函式用矩陣標準型求矩陣函式的具體步驟如下:
(1)設方陣A相似於對角陣,即
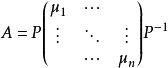 矩陣函式
矩陣函式,其中矩陣內的值是A的n個特徵值,則
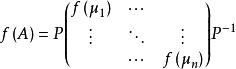 矩陣函式
矩陣函式(2)當A不能與對角陣相似時,則A必與Jordan標準型相似,設
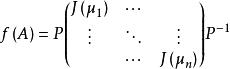 矩陣函式
矩陣函式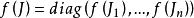 矩陣函式
矩陣函式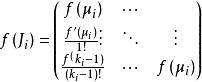 矩陣函式
矩陣函式最後
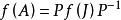 矩陣函式
矩陣函式利用最小多項式
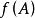 矩陣函式
矩陣函式用最小多項式求矩陣函式的具體步驟如下:
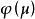 矩陣函式
矩陣函式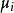 矩陣函式
矩陣函式第一步 計算矩陣A的最小多項式,確定其次數m及特徵值;
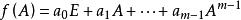 矩陣函式
矩陣函式第二步 設,確定出係數;
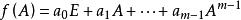 矩陣函式
矩陣函式第三步 代入可求得。

