定義描述
 齊次函式
齊次函式把函式的自變數乘以一個因子,如果此時因變數相當於原函式乘以這個因子 的冪,則稱此函式為 齊次函式。
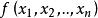 齊次函式
齊次函式 齊次函式
齊次函式定義函式 為 次齊次函式,需滿足關係:
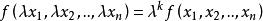 齊次函式
齊次函式歐拉定理
 齊次函式
齊次函式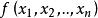 齊次函式
齊次函式對於 次齊次函式 ,有齊次函式的歐拉定理:
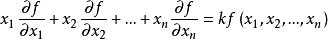 齊次函式
齊次函式定理證明:
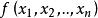 齊次函式
齊次函式 齊次函式
齊次函式因為函式為次齊次函式,所以對定義式兩邊求全微分有
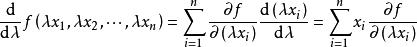 齊次函式
齊次函式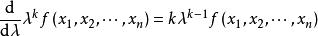 齊次函式
齊次函式這兩個全微分的值必相等,於是
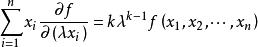 齊次函式
齊次函式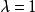 齊次函式
齊次函式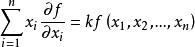 齊次函式
齊次函式取,得到
證畢。
齊次方程 :
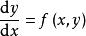 齊次函式
齊次函式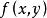 齊次函式
齊次函式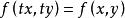 齊次函式
齊次函式如果方程 右端的函式 為它的變數的零次齊次函式,即滿足恆等式
那么稱上述方程為齊次方程。
例子
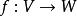 齊次函式
齊次函式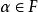 齊次函式
齊次函式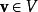 齊次函式
齊次函式線性函式是一次齊次函式,因為根據線性的定義,對於所有的和,都有:
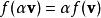 齊次函式
齊次函式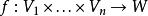 齊次函式
齊次函式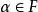 齊次函式
齊次函式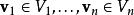 齊次函式
齊次函式多線性函式是n次齊次函式,因為根據多線性的定義,對於所有的和都有:
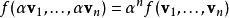 齊次函式
齊次函式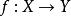 齊次函式
齊次函式從上一個例子中可以看出,兩個巴拿赫空間X和 Y之間的函式的n階弗雷歇導數是n次齊次函式。
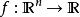 齊次函式
齊次函式n元單項式定義了齊次函式。
例如:
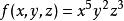 齊次函式
齊次函式是10次齊次函式,因為:
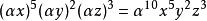 齊次函式
齊次函式。
齊次多項式是由同次數的單項式相加所組成的多項式。例如:
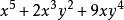 齊次函式
齊次函式是5次齊次多項式。齊次多項式可以用來定義齊次函式。
套用
對於以下的微分方程
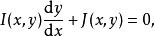 齊次函式
齊次函式其中I和 J是同次數的齊次函式,利用變數代換v=y/x,可以把它化為可分離變數的微分方程:
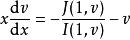 齊次函式
齊次函式。

