齊次微分方程

齊次微分方程（homogeneous differential equation）是指能化為可分離變數方程的一類微分方程，它的標準形式是 y'=f(y/x)，其中 f 是已知的連續方程。求解齊次微分方程的關鍵是作變換 u=y/x ，即 y=ux ，它可以把方程轉換為關於 u 與 x 的可分離變數的方程，此時有 y'=u+xu'，代入原方程即可得可分離變數的方程 u+xu'=f(u) ,分離變數並積分即可得到結果，需要注意的是，最後應把 u=y/x 代入，並作必要的變形。

基本信息

• 中文名：齊次微分方程
• 英文名：homogeneous differential equa-lion
• 定義：是指能化為可分離變數方程的一類微分方程
• 計算公式：y'=f(y/x)

• 求解關鍵：作變換 u=y/x ，即 y=ux
• 注意事項：最後應把u=y/x代入，並作變形
• 套用學科：高等數學

定義

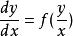齊次微分方程

形如 的一階微分方程稱為齊次微分方程，簡稱微分方程。

方程特點

齊次微分方程

齊次微分方程的特點是其右端項是以為變元的連續函式。

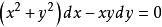齊次微分方程

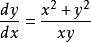齊次微分方程

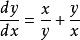齊次微分方程

例如， 是齊次微分方程，它可以轉化為：，即。

方程的解

齊次微分方程通過變數代換，可化為可分離變數微分方程來求解。

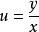齊次微分方程

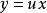齊次微分方程

令或，

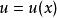齊次微分方程

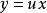齊次微分方程

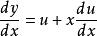齊次微分方程

其中是新的未知函式，對兩邊求導，則有：，

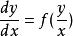齊次微分方程

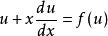齊次微分方程

將其代入，得：，

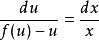齊次微分方程

分離變數，得：

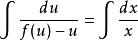齊次微分方程

兩邊積分，得：，

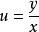齊次微分方程

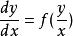齊次微分方程

求出積分後，再將回代，便得到方程的通解。

求解步驟

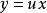齊次微分方程

（1）作變換，將齊次方程轉化為分離變數的微分方程；

（2）求解可分離變數的微分方程；

齊次微分方程

齊次微分方程

（3）用代替步驟（2）中所求通解中的（即變數還原），就可以得到原方程的通解。

注意事項

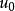齊次微分方程

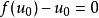齊次微分方程

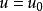齊次微分方程

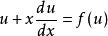齊次微分方程

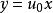齊次微分方程

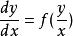齊次微分方程

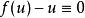齊次微分方程

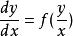齊次微分方程

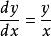齊次微分方程

如果有，使得，則顯然也是方程的解，從而也是方程的解；如果，則方程變成，這是一個可分離變數微分方程。

典例

例1

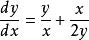齊次微分方程

求解方程。

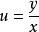齊次微分方程

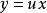齊次微分方程

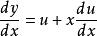齊次微分方程

解：令，則，，

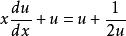齊次微分方程

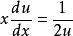齊次微分方程

原方程變為：，即；

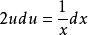齊次微分方程

分離變數可得：，

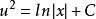齊次微分方程

左右兩端同時積分可得：，

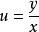齊次微分方程

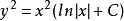齊次微分方程

將 代入，便可得到原方程的通解為：，其中 C 為任意常數。

例2

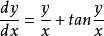齊次微分方程

求方程的通解。

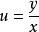齊次微分方程

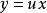齊次微分方程

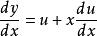齊次微分方程

解：令，則，，

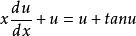齊次微分方程

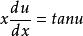齊次微分方程

原方程變為：，即；

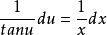齊次微分方程

分離變數可得：，

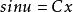齊次微分方程

左右兩端同時積分可得：，

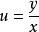齊次微分方程

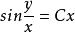齊次微分方程

將 代入，便可得到原方程的通解為：，其中 C 為任意常數。