歷史來源
齊奧爾科夫斯基公式早在1883 年,齊奧爾科夫斯基就《自由空間》一文中提出了關於宇宙飛 船的最初設計方案,顯示了他對宇宙航行的天才構想。
於1898年完成了航天學經典論文《利用噴氣工具研究宇宙空間》，但這篇論文直到1903年才在莫斯科的《科學評論》雜誌上發表。一般人認為，這篇論文的發表標誌著航天學理論的誕生。接著，他又於1910年、1911年、1912年、1914年在《航空報告》上發表了多篇關於火箭理論和太空飛行的論文，涉及到火箭運動、火箭發動機、火箭推進劑、火箭飛行控制、失重與超重、宇宙飛船設計、航天套用等各個方面，較為系統地建立起了火箭運動和航天學的理論基礎。
這些篇論文的發表,在人類的航天 科學史上起到了劃時代的重要作用。 首先,作者在論文中提出了用什麼樣的飛行器進入宇宙空間的問題。現在 我們已經知道在宇宙空間的空氣極為稀薄,幾乎接近真空,所以靠空氣浮力為力 源的氣球與氣艇都無法飛出大氣層。齊奧爾科夫斯基也意識到了這一點,所以在他的論文一開始就寫道:“裝有自動觀察儀的無人操縱的小型氣球,直到現在它的 升限也未能超過 22 公里。很明顯,利用氣球飛往更高空間的困難將隨著高度的 增大而不斷增加,要利用氣球或飛艇飛到大氣層範圍之外是完全不可能的。” 隨後,齊奧爾科夫斯基又認真地研究了利用大炮炮彈飛向宇宙的可能性。 他通過仔細的計算,最終認為利用炮彈飛往星際空間也是不可能的。這是因為炮 彈由大炮發射出時的初速度非常高,這就會在極短的時間內產生極大的動力加速 度,但這種加速度將會造成太空人的突然死亡以及儀器的徹底損壞。很顯然,大炮的炮彈根本不能用於星際航行。最後他得出了自己的結論:“我建議使用噴氣裝置,也就是火箭之類的飛行器去研究外層空間用以代替氣球和大炮炮彈。” 噴氣式火箭,離開地面的初始速度並不是需要太高,而是在飛行過程中逐漸加速的,最終達到足以擺脫地球引力,從而飛出地球大氣層的速度。因為宇航火箭的速度是逐漸提升的,加速度遠比炮彈小得多,所以就能夠保證火箭內乘員的 生命安全以及工作儀器的正常運轉。 但是,宇宙火箭在宇宙空間是如何飛行的呢?它的構造又應是怎樣的呢? 通過什麼辦法才能夠計算出宇宙火箭的飛行速度與高度呢?為了解決這些問題, 齊奧爾科夫斯基在物體運動力學理論方面進行了新的探索。他根據已知的力學原理全面地研究了火箭的運動過程,從而創立了牛頓古典力學中新的一章——變質量力學。他通過自己的研究,提出了著名的火箭推進速度的計算公式?齊奧爾科夫 斯基公式
1903年齊奧爾科夫斯基寫成的《利用噴氣工具研究空間》，在宇宙航行方面具有開拓性。他推論出在不考慮空氣動力和地球引力的理想情況下計算火箭在發動機工作期間獲得速度增量的公式，即
V=vln(m/m)
式中V為速度增量，v為噴流相對火箭的速度，m和m分別為發動機工作開始和結束時的火箭質量。速度增量稱為理想速度或特徵速度。用這個公式可以近似地估計火箭需要攜帶的推進劑的數量以及發動機參數對理想速度的影響。
當火箭運動速度接近光速時，計算理想速度則須利用相對論的原理，相應的公式是：
m/m=[(c+v)/(c-v)]^(c/2v)
式中c=299792.458km/s,為光速。這個公式稱為阿克萊公式，又稱廣義齊奧爾科夫斯基公式，只有以接近光速的星際航行，相對論效應不可忽略時才會用到它。
公式
齊奧爾科夫斯基火箭方程的核心內容是：基於動量守恆原理，任何一個裝置，通過一個消耗自身質量的反方向推進系統，可以在原有運行速度上，產生並獲得加速度。
其認為，任何一次飛行器軌道變化（速度變化）或者多次軌道變化都遵循如下公式:
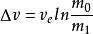齊奧爾科夫斯基公式其還可以寫成如下方式：
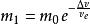齊奧爾科夫斯基公式或者
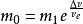齊奧爾科夫斯基公式或者
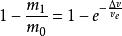齊奧爾科夫斯基公式其中：
m是火箭加速前的純質量總合，即初始總質量(該質量指，不含火箭可能攜帶的彈頭或者衛星等附加設施，僅為火箭自身各種子系統的綜合，後文中所有初始總質量都是指火箭純質量的總合）。
m是火箭加速後的純質量的總和。
v是火箭排氣速度(火箭噴射速度)，該速度與時間、地球重力加速度。
Δ v是火箭加速後速度與加速前速度的差值，它是對由且僅由火箭發動機產生的加速度求時間的積分得來。
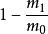齊奧爾科夫斯基公式是質量分率（質量比重）。
請注意，如上公式是在理想狀態下的推導結果，換句話說，實際過程中，在重力加速度和各種干擾力的聯合作用下， 通常並不是如上公式計算所得。
齊奧爾科夫斯基公式欲解決的問題：如何解釋固體、液體燃料火箭能助人類從地表發射，並擺脫行星引力，深入宇宙。
前提條件：不考慮空氣阻力（實際上在大氣層內有），不考慮地球引力（這使此公式可以分析深空中火箭的速度問題），對象是使用固體或者液體燃料的火箭。齊奧爾科夫斯基公式不能用來解釋“無工質”動力裝置驅動飛船的運動。
爭議
雖然由英國著名數學家威廉·摩爾（William Moore ）名為“關於火箭運動的論述”（英語：A Treatise on the Motion of Rockets）顯示，英國皇家軍事學院已於公元1813年推導出該原理，並套用於最初的武器研究，但由於該理論從未公開發表，故不被承認。另一方面，由於現知的公式是由康斯坦丁·艾多爾道維奇·齊奧爾科夫斯基於公元十九世紀末獨立推導，並首次公開發表，且該火箭方程式已在世界範圍內被廣泛承認。故該火箭方程式的名稱，仍然繼續使用原有名稱：齊奧爾科夫斯基火箭方程式。
公式特點
那就是火箭所能達到的速度可以高於噴射物的噴射速度。 這一點之所以重要, 是因為它表明 我們可以通過較低的噴射速度來達到太空飛行器所 需要的高速度, 這在技術上要遠比直接達到高速度來得容易。 但是火箭雖然能夠達到比噴射物噴射速度更高的速度, 但為此付出的代 價卻也不小。 因為火箭所要達到的速度 越高,其初始質量與推進過程完成後 的質量之比 就必須越大,從而火箭的有效載荷就必須越小。 這是齊奧爾 科夫斯基公式的第二個重要特點。 最糟糕的是, 齊奧爾科夫斯基公式是一個對 數關係式, 這是增長極其緩慢的關係式, 它的出現表明燃料數量的增加 m。的增加對速度增加所起的作用非常有限。 這一點極大地限制了火箭的 運載效率。 那么, 有沒有什麼辦法可以改善火箭的運載效率呢? 齊奧爾科夫斯基提 出了多級火箭的構想。多級火箭就是把幾個單級火箭連線在一起形成的,其中的 一個火箭先工作,工作完畢後與其他的火箭分開,然後第二個火箭接著工作,依此 類推。由幾個火箭組成的就稱為幾級火箭,如二級火箭、三級火箭,等等。多級火 箭的優點是每過一段時間就把不再有用的結構拋棄掉,無需再消耗推進劑來帶著 它和有效載荷一起飛行。因此,只要在增加推進劑質量的同時適當地將火箭分成 若干級,最終可以使火箭達到足夠大的運載能力。 多級火箭的好處, 是在每一級的燃料用盡後可以把該級的外殼拋棄, 而減輕下一級所負載的質量。不過, 多級火箭雖然有較高的運載效率, 但它在 技術上的複雜性也較高。 因此在實際使用時, 人們往往在運載效率與技術複雜 性之間作折中, 三級火箭就是最常見的折中結果。 即便使用多級火箭, 為了將 幾噸的有效載荷送入近地軌道, 通常也需要發射質量為幾百噸的火箭 比如發射 “神舟號” 飛船的長征二號 型火箭的發射質量約為四百八十噸,近地軌道的 有效載荷則為八噸左右。 這種巨大的消耗, 使得航天發射的費用極其高昂。 果你想到近地軌道上的國際空間站去遨遊一下的話,大約要準備兩千萬美元的 費用。
套用
火箭是以熱氣流高速向後噴出,利用產生的反作用力向前運動的噴氣推進 裝置。它自身攜帶燃燒劑與氧化劑,不依賴空氣中的氧助燃,既可在大氣中,又可 在外層空間飛行。火箭在飛行過程中隨著火箭推進劑的消耗,其質量不斷減小, 是變質量飛行體。現代火箭可用作快速遠距離運送工具,如作為探空、發射人造 衛星、載人飛船、空間站的運載工具,以及其他飛行器的助推器等。如用於投送 作戰用的戰鬥部彈頭,便構成火箭武器。其中可以制導的稱為飛彈,無制導的稱 為火箭彈。 火箭是目前唯一能使物體達到宇宙速度,克服或擺脫地球引力,進入宇宙 空間的運載工具。火箭的速度是由火箭發動機工作獲得的。由這個公式可知,火 箭的速度與發動機的噴氣速度成正比,同時隨火箭的質量比增大而增大。即使使 用性能最好液氫液氧推進劑,發動機的噴氣速度也只能達到4.3~4.4 公里/秒。因 此,單級火箭不可能把物體送入太空軌道,必須採用多級火箭,以接力的方式將航 天器送入太空軌道。
公式知識延伸
齊奧爾科夫斯基是現代宇宙航行學的奠基人。被稱為航天之父,他最先論證了利用火箭進行星際交通、製造人造地球衛星和近地軌道站的可能性，指出發展宇航和製造火箭的合理途徑，找到了火箭和液體發動機結構的一系列重要工程技術解決方案，他有一句名言:"地球是人類的搖籃，但人類不可能永遠被束縛在搖籃里。"
走向太空，宇宙的浩瀚是星際旅行家們面臨的最基本的事實。 即使能夠達到接近光 速的速度, 飛越恆星際空間所需的時間仍然是極其漫長的。 從地球出發, 飛到銀河系的中心約需要三萬年的時間, 飛到仙女座星雲 M31 河外星系約需要二百二十萬年的時間, 而到室女座星系團 Virgo 河外星系團則需要約六千萬年的時間相對於人類彈指一瞬的短暫生命來說, 這些時間顯然都太漫長了。 但是幸運的是, 所有這些時間都是在靜止參照系中測量的。 相對論中有一個著名的時鐘延緩效應, 它表明運動參照系中的時間流逝會比靜止參照系中測量到 火箭的飛行速度越高,這種時鐘延緩效應就越可觀, 太空人所感受到的時間流逝也就越緩慢。 考慮到這個因素, 太空人是不是有可能在自己的有生之年到銀河系的中心、仙女座星雲、甚至室女座星系團去旅行呢?答案是肯定的，我們考慮一個非常簡單的情形,即火箭始終處於勻加速過程之中，不用說, 這種火箭耗費的能量將是極其驚人的, 不過這裡我們姑且把技術上的困難拋在一邊, 只討論理論上的可能性。 同時, 我們把火箭的加速度選為與地球表面的重力加速度一樣這樣, 太空人在飛船上感受到的重力環境就與地球表面一樣, 不會象我們在電視上看到的那樣在飛船內隨意飄蕩, 並且假定火箭在後半程做減速運動 這樣,太空人才能在目的地著陸。 在這樣的飛行條件下, 如果飛行距 離非常大 遠遠大於一光年, 飛船上的時間流逝，這裡時間以年為單位, 航程則以光年為單位。 這個公式與齊奧爾科夫斯基公式一樣, 也出現了以增長緩慢著稱的對數函式。 只不過, 基公式中,對數函式的出現是一件不幸的事情, 因為它限制了火箭速度的增加, 從而限制了火箭的運載效率; 而在現在這個公式中, 對數函式的出現卻成了一 件幸事, 因為它延緩了飛船上的時間流逝, 從而極大地擴展了太空人在有生之年可以飛越的距離。
