概念
高德納箭號表示法是種用來表示很大的整數的方法，由高德納於1976年設計。它的意念來自冪是重複的乘法，乘法是重複的加法。
定義
見右圖。
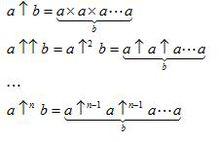高德納箭號表示法計算
一個箭頭
2↑3=2×2×2=8
2↑4=2×2×2×2=16
3↑3=3×3×3=27
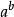高德納箭號表示法a↑b=
兩個箭頭
2↑↑3=2↑2↑2（注意：此處要從右往左計算）=2↑4=16
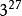高德納箭號表示法3↑↑3=3↑3↑3=3↑27==7625597484987
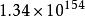高德納箭號表示法4↑↑3=4↑4↑4=4↑256≈
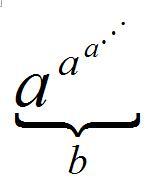a↑↑ba↑↑b=
三個箭頭
2↑↑↑3=2↑↑2↑↑2=2↑↑2↑2=2↑↑4=2↑2↑2↑2=2↑2↑4=2↑16=65536
3↑↑↑3=3↑↑3↑↑3=3↑↑7625597484987=3^3^3^3……（7625597484987個3）
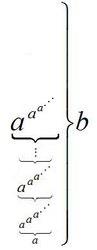高德納箭號表示法a↑↑↑b=
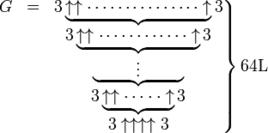
葛立恆數
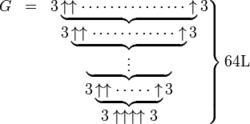高德納箭號表示法葛立恆數的定義見右邊
首先來看最下面，是g1=3↑↑↑↑3，就是3↑↑↑3↑↑↑3=3↑↑↑（3↑↑3↑↑3）
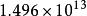高德納箭號表示法而3↑↑3↑↑3本來就是由7625597484987個3組成的指數塔了，地球到太陽的距離是厘米，也就是說如果把這個指數塔每隔2厘米寫下來，可以從地球一直寫到太陽。
那么g1=3↑↑↑B=3↑↑3↑↑3↑↑3……（有B個3）。
大家已經知道，僅僅4個↑就已經搞出一個大得不可理喻的數字了，那么現在我們來看一下葛立恆數的第二層，也就是3↑↑↑↑3上面那一層：
g2=3↑↑↑……↑3，有g1個箭頭，注意，不是g1個3，不是g1層指數塔，甚至不是g1個指數塔層的指數塔，而是g1個箭頭！！箭頭！！簡直有種美漫開掛不打草稿的感覺......
葛立恆數總共有64層，每一層中的箭頭個數都由前一層得出。所以葛立恆數簡單說來就是一個指數塔的指數塔的箭頭塔...吧... 總之只可意會不可言傳...
那么葛立恆數到底有多大呢？沒人知道，也沒人知道這個數有多少位數字，甚至也沒人知道葛立恆的位數的位數有多少位數（此處有阿伏伽德羅常數個“位數”）...我們只知道它的後幾百位數，其中末位數是7. ，葛立恆數秒天秒地~當然首先你得解釋得清咯...
