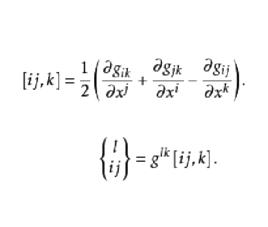定義
第一種克里斯托費爾符號：
克里斯托費爾符號①
第二種克里斯托費爾符號：
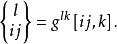克里斯托費爾符號②
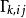克里斯托費爾符號
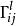克里斯托費爾符號
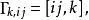克里斯托費爾符號
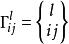克里斯托費爾符號有不少書籍，尤其是歐洲的書籍，用 和 表示第一種和第二種克里斯托費爾符號，即 。
克里斯托費爾符號引入的這兩種符號，是否是張量，待討論了它們的變換律即可斷定。兩種符號中的指標除一個(如 )看作是上標外，其餘的都看作下標，它們適用於一個上標和一個下標的求和約定。
克里斯托費爾符號將式②內乘以 ，得
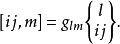克里斯托費爾符號
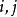克里斯托費爾符號從定義可知，這兩種符號對於 都是對稱的，即
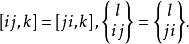克里斯托費爾符號④
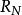克里斯托費爾符號
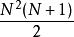克里斯托費爾符號
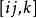克里斯托費爾符號於是在N維黎曼空間 中，都各有 個獨立的分量。例如，對於N=3而言， 有18個獨立分量：
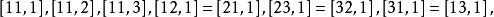克里斯托費爾符號
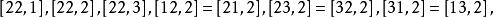克里斯托費爾符號
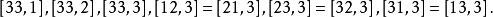克里斯托費爾符號
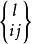克里斯托費爾符號對於 也類似地有18個獨立的分量。
用克里斯托費爾符號表示基本張量的導數
(1) 由式①，有
克里斯托費爾符號改變啞標，有
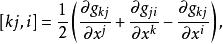克里斯托費爾符號
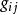克里斯托費爾符號因為 是對稱張量，將以上兩式相加，得
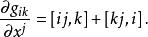克里斯托費爾符號⑤
(2) 因為
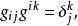克里斯托費爾符號
克里斯托費爾符號對微分，得
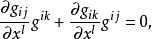克里斯托費爾符號
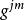克里斯托費爾符號內乘以 ，有
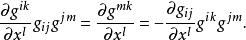克里斯托費爾符號將式⑤和式②代入上式得
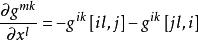克里斯托費爾符號
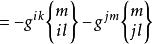克里斯托費爾符號
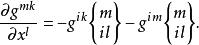克里斯托費爾符號⑥
克里斯托費爾符號的變換率
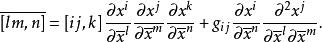克里斯托費爾符號⑦
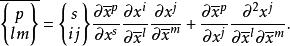克里斯托費爾符號⑧
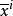克里斯托費爾符號
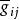克里斯托費爾符號
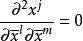克里斯托費爾符號式⑦與式⑧給出了兩種克里斯托費爾符號的變換律，符號上方的橫線表示它是在坐標系 里對於基本張量 計算的。變換關係表明兩種克里斯托費爾符號都不是張量。可是在坐標的線性變換中，在 這種十分特殊的情況下，這兩種符號的變換律就像張量的變換律一樣。
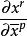克里斯托費爾符號將式⑧兩邊內乘以 ，得
克里斯托費爾符號⑨
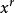克里斯托費爾符號
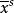克里斯托費爾符號這是用 對 的一階偏導數和第二種克里斯托費爾符號表示二階偏導數的一個重要方程，常用到這個關係。
