簡介
在數學裡面， 疊代冪次（亦作 超-4運算），或可理解為疊代乘方、冪塔運算和超冪運算、廣義冪指函式 等，是專指冪的下一個超運算級別。以下列舉了首四個超運算級別，其中 疊代冪次為第四級。
定義
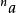疊代冪次對於任何正實數 a及非負整數 n， 被定義為：
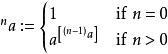疊代冪次疊代乘方
通常的解釋是：
x+x+x=x*3，此3為表示3個相同的x相加；
x*x*x=x^3，此3表示相同的3個x相乘；
x^(x^x)=x^^3，此3表示連續3個x冪指運算且“^^”為新的運算。
可以繼續推廣。這就是疊代冪次的來由 。
從上述定義中可見，當計算被表達成 冪塔的 疊代冪次時，冪運算是先由最深層（以符號來表示，則最高級）的 上標數做起。
例子如下：
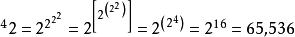疊代冪次要注意，冪是不遵從結合律的，因此以其他順序來計算上述表達式將會出現不一樣的答案，例如：
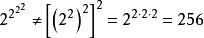疊代冪次因此， 冪塔一定要從上而下（或從右至左）來運算。在電腦程式中，此制式稱為 右結合律。
疊代冪次有多種表示方法，通常有：
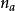疊代冪次標準符號記法： a[4]n 或者；高納德箭號表示法： a↑↑n；ASCII符號： a^^n；
其他如疊代指數法、阿克曼函式法、Hooshmand符號記法、超運算符號等不再贅述。
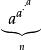疊代冪次當 a與 n為互質時，我們可以透過歐拉定理來計算 的最後 m個小數位值。
一般的，x^^0.5 是沒有定義的（注意，它不等於x^0.5）。可以用一個假設解決此問題 。
相關條目
•阿克曼函式
•超運算
