簡介
期望報酬率(Expected rate of return):是指各種可能的報酬率按機率加權計算的平均報酬率,又稱為預期值或均值。它表示在一定的風險條件下,期望得到的平均報酬率。
特徵
期望報酬率反映的是預期收益率的平均化,不能直接用來衡量風險。
期望報酬率的計算
如表所示,將各種可能結果與其所對應的發生機率相乘,並將乘積相加,則得到各種結果的加權平均數。此處權重係數為各種結果發生的機率,加權平均數則為期望報酬率。
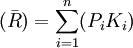 期望報酬率
期望報酬率期望報酬率的計算公式為:
式中,為期望報酬率;Pi為第i種結果出現的機率;n為所有可能結果的數目。
例:ABC公司有甲、乙兩個投資項目,假設未來的經濟情況有三種:繁榮、正常與衰退,有關的機率分布和預期報酬率見表1,計算甲、乙項目的期望報酬率。
表 ABC公司項目投資未來收益狀態分布表
| 經濟狀況 | 發生機率 | 甲項目預期報酬率 | 乙項目預期報酬率 |
| 繁榮 正常 衰退 | 0.3 0.4 0.3 | 90% 15% -60% | 20% 15% 10% |
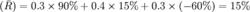 甲:
甲: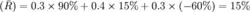 乙:
乙:兩者的期望報酬率相同,但其機率分布不同。甲項目報酬率的分散程度大,變動範圍在-60%~90%之間;乙項目報酬率的分散程度小,變動範圍在10%~20%之間。這說明兩個項目的報酬率相同,但風險程度不同。