面積射影定理

面積射影定理（Planar mapping theorem）是一個數學定理，是指平面圖形射影面積等於被射影圖形的面積S乘以該圖形所在平面與射影面所夾角的餘弦。

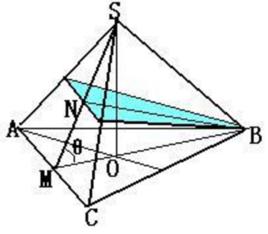
定理概述

如圖，設平面 α外的△ABC在平面 α內的射影為△ABO，分別記△ABC的面積和△ABO的面積為S和S′，記△ABC所在平面和平面α所成的二面角為θ，則 cosθ=S′︰S．

證明

定理證明思路：因為射影就是將原圖形的長度（三角形中稱高）縮放，所以寬度是不變的，又因為平面多邊形的面積比=邊長的平方比。所以就是圖形的長度（三角形中稱高）的比。那么這個比值應該是平面所成角的餘弦值。在兩平面中作一直角三角形，並使斜邊和一直角邊垂直於棱（即原多邊形圖的平面和射影平面的交線），那么三角形的斜邊和另一直角邊就是其多邊形的長度比，即為平面多邊形的面積比，而將這個比值放到該平面三角形中去運算，即可。

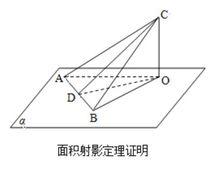面積射影定理

證明：如上圖，作△ABC的AB邊上的高CD，垂足為D，連OD，易知OD⊥AB，故∠CDO即為二面角C-AB-O的平面角，即∠CDO=θ．

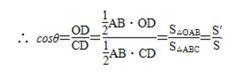面積射影定理的證明