邊界層方程數值解法

邊界層理論是德國L.普朗特在20世紀初建立起來的。當流體流經物體表面時，靠近壁面邊界很薄的一層，粘性效應很重要。利用粘性邊界層很薄的特點，可以把流體力學運動方程（即納維－斯托克斯方程）中量級較小的各項忽略掉，簡化成為邊界層方程。邊界層理論為粘性流體力學的套用開闢了廣闊的道路，在近代力學中起著重要的作用。

正文

以平面問題為例：定常二維不可壓縮流的邊界層方程組，由一個連續性方程和兩個動量方程組成，即 式中u、v為沿著x、y方向上的速度分量;p、ρ和v分別表示壓力、密度和運動粘性係數。邊界條件要求在不滲透的固體表面上，兩個速度分量為零。在邊界層外緣,u漸近地等於外緣速度ue(x)，所以有：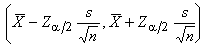

(2)

另外,還要給定壓力梯度дp/дx。由於式(1c)中的壓力p只是x的函式，它與外緣速度之間的關係為：

。

方程組(1)是非線性偏微分方程組，求解很困難,一般需用數值方法，這裡主要介紹相似性解法和差分解法。
相似性解法　其要點是引進無量綱相似參數，將偏微分方程轉換成常微分方程,然後再用數值方法求解。德國Н.布拉西烏斯在1907年首次用此法解壓力為常數的平板繞流問題。在連續性方程中引進流函式Ψ，即u=дΨ/дy，v=-дΨ/дx,並定義一個相似參數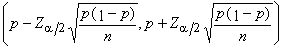同時令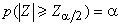f(η) 為無量綱的流函式。速度分量u、v及其導數дu/дy和д2u/дy2均可以從Ψ 求出，而且都可以用函式 f(η)及其高階導數表示。最後，原方程組(1)變成一個三階常微分方程：

f冺＋ff″＝0， (3)

對應於邊界條件(2), 要求f(0)＝f′(0)＝0,f′(∞)＝1。這是兩點邊值問題。一般的作法是先假設f″(0)＝α, 從η＝0的地方對方程(3)進行數值積分。當η→∞時，要求f′(η)→1。如果條件不能滿足，必須更改 α的初值，反覆疊代到滿足 f′(∞)＝1的條件為止。但通過變數的轉換，也可將這個兩點邊值問題換成初值問題，求解時不需要反覆疊代。令ζ=α1/3η,α仍然代表f″(0);再令f(η)=α1/3F(ζ),則f′(η)=α2/3F′(ζ),f″(η)=αF″(ζ)，f冺(η)=α4/3F冺(ζ)。代入方程式(3)，得到一個同樣形式的方程：
F冺(ζ)+F(ζ)F″(ζ)=0，(4)
但邊界條件有些不同，變成F(0)＝F′(0)＝0，F″(0)＝1三個初始條件，正好用數值積分直接求F(ζ)，而後利用f′(∞)=1=α2/3F′(∞)求α，即

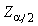(5)

方程(4)的具體解法， 是把它改為三個一階常微分方程，令F的一階導數為G，二階導數為H，則有：
F′＝G，G′＝H，H′＋FH＝0， (6)
F、G、H為三個未知變數，相應的初始條件為：F(0)＝0，G(0)＝0，H(0)＝1。這組一階常微分方程可用一般的數值積分法求解。
差分解法　這種解法是將微分算符近似地用差商代替，把微分方程改為差分方程然後再求解。在有壓力梯度的流動中，相似條件不能滿足。用前面相同的坐標變換,即但此處應令由於相似性假設不適用,流函式f是ξ、η的函式。通過坐標轉換，方程(1b)變為：　

,(7)

式中 f′、f″、f冺 均為 η 的導數；f 為 ξ 的導數；為壓力梯度參數。差分－微分方程是將上式的 ξ導數項改用差分形式，而在η方向仍保持微分形式。這樣，方程(7)變成在 η 方向上的常微分方程，具有在η＝0，η＝∞的兩點邊界條件,可用疊代法求解。近來，人們直接將邊界層方程的所有偏導數均用差分表示。這類差分法的格式很多（見有限差分方法），現以凱勒的差分格式為例。 此法首先將原方程〔如方程(7)〕改寫成幾個一階偏微分方程組，而後將所有一階導數均用中心差分，給出具有二階精度的差分方法。現將 f(ξ，η)對 η的一階導數用 g(ξ，η)表示，二階導數用h(ξ，η)表示。方程(7)可改為：
　 (8a)

。 (8b)

上兩式均在點上取值,它們的差分方程為：
(9a)

(9b)

方程(8b)則在點上取值，如
　
　
　
　 在這些式子中，還有一些非線性項，如g卾,(fh)i+1,須進行線性化，如果把gi+1和gi的差值看作小量,並忽略小量二階以上的項，即得出線性化關係式：
　 將以上各式代入(8b),即可得出在i+1截面上的線性差分方程。連同(9a)和(9b)一起,並結合相應的邊界條件,便可聯立求解三個未知量f、g和h。從f即可求流函式Ψ,從而可計算出兩個速度分量u和v。

配圖

相關連線