高斯定理定義
通過任意閉合曲面的電通量等於該閉合曲面所包圍的所有電荷量的代數和與電常數之比。套用學科:電力(一級學科);通論(二級學科)
定理內容
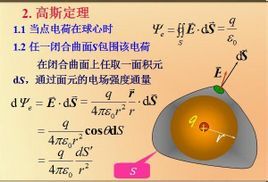
矢量分析的重要定理之一。穿過一封閉曲面的電通量與封閉曲面所包圍的電荷量成正比。換一種說法:電場強度在一封閉曲面上的面積分與封閉曲面所包圍的電荷量成正比。由於磁力線總是閉合曲線,因此任何一條進入一個閉合曲面的磁力線必定會從曲面內部出來,否則這條磁力線就不會閉合起來了。如果對於一個閉合曲面,定義向外為正法線的指向,則進入曲面的磁通量為負,出來的磁通量為正,那么就可以得到通過一個閉合曲面的總磁通量為0。這個規律類似於電場中的高斯定理,因此也稱為高斯定理
電場強度E 在任意面積上的面積分 稱為電場強度對該面積的通量。根據庫侖定律可以證明電場強度對任意封閉曲面的通量正比於該封閉曲面內電荷的代數和,即
稱為電場強度對該面積的通量。根據庫侖定律可以證明電場強度對任意封閉曲面的通量正比於該封閉曲面內電荷的代數和,即
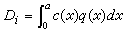 , (1)
, (1)
高斯定理反映了靜電場是有源場這一特性。凡是有正電荷的地方,必有電力線發出;凡是有負電荷的地方,必有電力線會聚。正電荷是電力線的源頭,負電荷是電力線的尾閭。
高斯定理是從庫侖定律直接導出的,它完全依賴於電荷間作用力的二次方反比律。把高斯定理套用於處在靜電平衡條件下的金屬導體,就得到導體內部無淨電荷的結論,因而測定導體內部是否有淨電荷是檢驗庫侖定律的重要方法。
對於某些對稱分布的電場,如均勻帶電球的電場,無限大均勻帶電面的電場以及無限長均勻帶電圓柱的電場,可直接用高斯定理計算它們的電場強度。
當存在電介質並用電位移D描寫電場時,高斯定理可表示成
 。 (2)
。 (2)
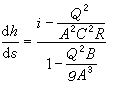 , (3)
, (3)
高斯定理的微分形式為
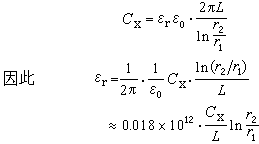 。
。
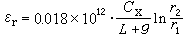 。
。
高斯定理延伸
高斯定理2
(代數學基本定理)
定理:凡有理整方程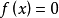 至少有一個根。
至少有一個根。
推論:一元n次方程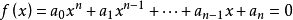
高斯定理3
(數論)
正整數n可被表示為兩整數平方和的充要條件為n的一切形如4k+3形狀的質因子的冪次均為偶數。
電路基礎
| 電的發明是人類工業發展的開始;有了電世界才有今天的科技發達;社會繁榮! |