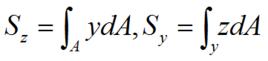簡介
矩有一階矩、二階矩以及更高階的矩,我們統稱高階矩,而最常用的則是一階矩和二階矩。
一階矩又叫靜矩,是對函式與自變數的積xf(x)的積分(連續函式)或求和(離散函式)。力學中用以表示f(x)分布力到某點的合力矩,幾何上可以用來計算重心,統計學中叫做數學期望(均值)。
平面圖形對指定軸線的靜矩等於微元面積與各微元至截面上指定軸線距離乘積的積分。
當坐標軸通過圖形的形心時,其靜矩為零;反之,若圖形對某軸的靜矩為零,則該軸必通過圖形的形心。
簡單推導
任意平面圖形如右圖所示,其面積為A,y 軸和 z 軸為圖形所在
 靜矩
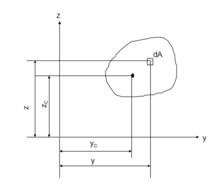
靜矩平面內的坐標軸,在坐標(y , z)處取微面積dA,遍歷整個圖形面積A的積分
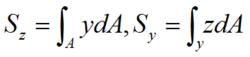 靜矩
靜矩(i.1)
分別定義為圖形對z軸和y軸的 靜矩,也稱為圖形對z軸和y軸的一次矩。
從 (i.1)看出,平面圖形的靜矩是對某一坐標軸而言的,不同圖形對不同的坐標軸,其靜矩也就不同。靜矩的數值可能為正,可能為負,也可能為零。靜矩的量綱為[長度] 。
構想有一個厚度很小的均質薄板,薄板的形狀與右圖中的平面圖形相同。顯然,在yz坐標系中,上述均質薄板的重心與平面圖形的形心有相同的坐標y和z由靜力學可知,薄板重心的坐標y和z分別為
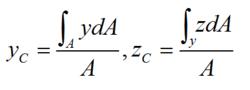 靜矩
靜矩(I.2)
這也就是確定平面圖形的形心坐標的公式。利用(i.1)可以把式(i.2)改寫成
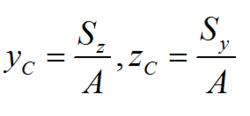 靜矩
靜矩(i.3)
所以,把平面圖形對z軸和y軸的靜矩,除以圖形的面積A,就得到了圖形形心的坐標y和z。把上式改寫成
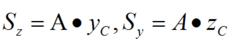 靜矩
靜矩(i.4)
這表明,平面圖形對z軸和y軸的靜矩分別等於圖形面積A乘形心的坐標y和z。
由以上兩式看出,若S=0和S=0,則y=0和z=0。可見,若圖形對某一軸的靜矩等於零,則該軸必通過圖形的形心;反之,若某一軸通過形心,則圖形對該軸的靜矩等於零。
(以上推導,部分參考了山東大學的馮維明老師所編寫《材料力學》一書,表示衷心感謝,亦在此註明,請勿抄襲)